Epita:Algo:Cours:Info-Sup:Ensembles
Sommaire |
Les ensembles
En plus de tester l'appartenance d'un élément à un ensemble, on doit pouvoir:
- ajouter un élément à un ensemble,
- supprimer un élément d'un ensemble,
- tester si l'ensemble est vide,
- etc.
Comme précédemment dit, nous accepterons la possibilité d'occurrences multiples des éléments (famille). Certaines des représentations évoquées seront utilisables uniquement par des ensembles et d'autres seront aussi valables pour des multi-ensembles. Commençons par donner le type algébrique abstrait des ensembles.
Le type ensemble
types
ensemble
utilise
élément, booléen
opérations
ensemblevide :ensemble ajouter : élément x ensemble
ensemble supprimer : élément x ensemble
ensemble _
_ : élément x ensemble
booléen
Pour les opérations ajouter et supprimer, il y a deux comportement possibles suivants que l'on considère le cas d'un élément à ajouter déjà présent ou celui d'un élément à supprimer absent de l'ensemble, ce qui donne les deux possibilités suivantes:
- On gère une erreur, ce qui implique que ces deux opérations sont partielles et dans ce cas nécessite une précondition,
- On considère alors ces deux opérations comme sans effet.
Dans les axiomes qui suivent, nous considérerons la deuxième proposition, c'est à dire que l'ensemble reste inchangé après une action sans effet.
axiomes
xensemblevide = faux x = y
(x
ajouter(y, e)) = vrai x ≠ y
(x
ajouter(y, e)) = (x
e) x = y
(x
supprimer(y, e)) = faux x ≠ y
(x
supprimer(y, e)) = (x
e)
Nous pouvons y ajouter l'opération qui retourne le nombre d'éléments de l'ensemble, soit:
opérations
card : ensembleentier
Cette dernière est définie partout, nous avons alors les axiomes suivants:
axiomes
card(ensemblevide) = 0 xe = vrai
card(ajouter(x, e)) = card(e) x
e = faux
card(ajouter(x, e)) = card(e) + 1 x
e = vrai
card(supprimer(x, e)) = card(e) - 1 x
e = faux
card(supprimer(x, e)) = card(e)
Remarque: Il serait tout aussi envisageable d'y ajouter les opérations classiques sur les ensembles telles que union, intersection, complémentaire et sous-ensemble.
Enumération d'un ensemble
Dans une liste, pour appliquer un même traitement à tous les éléments, on utilise un parcours séquentiel des éléments de cette liste. Dans un ensemble, on va plutôt choisir un élément, lui appliquer le traitement et recommencer sur l'ensemble obtenu en supprimant l'élément que l'on vient de traiter. On ajoute alors une opération de choix à la signature du type ensemble, ce qui donne:
opérations
choisir : ensembleélément
avec la précondition et l'axiome suivants:
préconditions
choisir(e) est-défini-ssi e ≠ ensemblevide
axiomes
choisir(e)e = vrai
L'algorithme traitant tous les éléments d'un ensemble donné, pourrait alors être le suivant:
algorithme procédure traitementcomplet
Paramètres locaux
ensemble e
Variables
élément x
Début
tant que e <> ensemblevide faire
x 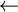 choisir(e) /* Choix de l'élément dans l'ensemble */
traiter(x) /* Application du traitement à l'élément choisi */
e
choisir(e) /* Choix de l'élément dans l'ensemble */
traiter(x) /* Application du traitement à l'élément choisi */
e 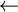 supprimer(x, e) /* Suppression de cet élément */
fin tant que
fin algorithme procédure traitementcomplet
supprimer(x, e) /* Suppression de cet élément */
fin tant que
fin algorithme procédure traitementcomplet
Remarque: Nous verrons un peu plus loin dans ce chapitre les différentes représentations possibles des ensembles.
Ensembles à occurrences d'éléments multiples (familles)
Dans ces cas là, on conserve les opérations précédentes, mais leur comportement diffère. En effet, l'ajout d'un élément existant augmente le nombre d'éléments de l'ensemble. De même la suppression d'un élément n'implique pas qu'il disparaisse de l'ensemble (s'il en existe plusieurs occurrences). On ajoutera alors une nouvelle opération (nboccurrences) qui permet de connaître le nombre d'occurrences d'un élément dans le multi-ensemble.
Ce qui donne le type algébrique abstrait suivant:
types
multiensemble
utilise
élément, booléen, entier
opérations
multiensemblevide :multiensemble ajouter : élément x multiensemble
multiensemble supprimer : élément x multiensemble
multiensemble _
_ : élément x multiensemble
booléen card : multiensemble
entier nboccurrences : élément x multiensemble
entier
axiomes
(xmultiensemblevide) = faux x = y
(x
ajouter(y, me)) = vrai x ≠ y
(x
ajouter(y, me)) = (x
me) nboccurrences(x, me) <= 1
(x
supprimer(x, me)) = faux x ≠ y
(x
supprimer(y, me)) = (x
me)
card(multiensemblevide) = 0 card(ajouter(x, me)) = card(me) + 1 xme = vrai
card(supprimer(x, me)) = card(me) - 1 x
me = faux
card(supprimer(x, me)) = card(me)
nboccurrences(x, multiensemblevide) = 0 x = ynboccurrences(x, ajouter(y, me)) = nboccurrences(x, me) + 1 x ≠ y
nboccurrences(x, ajouter(y, me)) = nboccurrences(x, me) nboccurrences(x, me) = 0
nboccurrences(x, supprimer(x, me)) = 0 nboccurrences(x, me) >= 1
nboccurrences(x, supprimer(x, me)) = nboccurrences(x, me) - 1 x ≠ y
nboccurrences(x, supprimer(y, me)) = nboccurrences(x, me)
Remarques:
- Comme pour les ensembles, Il serait tout aussi envisageable d'ajouter aux multi-ensembles les opérations classiques telles que union, intersection et complémentaire.
- L'énumération des éléments d'un multi-ensemble se fait à l'aide du même algorithme que pour un ensemble. La suppression n'enlevant qu'une seule occurrence de l'élément, le nombre d'élément correspond alors aux nombres total d'éléments, toutes occurrences confondues.
Représentation des ensembles
Il existe plusieurs manières d'implémenter les ensembles en mémoire, nous allons en présenter deux:
Représentation par des tableaux de booléens
Si le nombre possibles d'éléments N est fini, On peut représenter un ensemble à l'aide d'un tableau de N booléens. Ce qui donnerait la déclaration suivante:
Constantes
Nbmax = ...
Types
t_ensemble = Nbmax booléen /* Définition du tableau de booléens */
Variable
t_ensemble ens
Si l'élément i ∈ ens alors ens[i] = vrai et faux sinon. Le test d'appartenance à un ensemble se fait juste en regardant à l'index correspondant à l'élément s'il est vrai ou faux. L'insertion d'un élément ou la suppression d'un élément i se font elles en fixant respectivement ens[i] à vrai ou faux.
Remarque:
- Ces opérations sont faciles à implémenter et rapides puisqu'il n'y a qu'un accès à la donnée et éventuellement une affectation de valeur.
- En revanche le coût mémoire est important:
- surtout si N est grand et si peu d'éléments de l'ensemble sont présents. Le ratio d'occupation étant dans ce cas très faible.
- L'ensemble vide est représenté par un tableau où tous les éléments sont faux. Ce qui implique, d'ailleurs, que l'initialisation d'un ensemble vide demande N affectations de valeur.
- Même chose pour une énumération complète de tout l'ensemble.
Dans ce type de représentation, les correspondances entre les opérations abstraites et l’implémentation statique du type (pour un ensemble ens) sont les suivantes :
| Type abstrait | ⇔ | Représentation en tableau de booléens |
| ajouter( x, ens) | ens[x]=vrai | |
| supprimer(x,ens) | ens[x]=faux | |
| x ∈ ens | ens[x] | |
| ensemblevide | pour i=1 jusqu'à N faire : ens[i]=faux fin pour | |
| card(ens) | c=0 pour x=1 jusqu'à N faire : si ens[x] alors : : c=c+1 : fin si fin pour |
Remarque: Cette représentation doit être modifiée pour les multi-ensembles. En effet, dans ce cas on remplace les booléens par des entiers indiquants le nombre d'occurrences de l'élément.
Représentation par des listes
Lorsque le nombre d'éléments possibles est trop grand ou lorsque l'ensemble est infini, mais que les ensembles que l'on manipule sont assez petits, on peut les représenter sous forme de listes.
Dans ce cas, un ensemble de N éléments est représenté par une liste de N éléments.
Remarque: Dans la mesure où l'ordre des éléments n'a pas d'importance, il existe plusieurs listes possibles.
- le test d'appartenance d'un élément x à un ensemble ens (la recherche), se fait en parcourant séquentiellement la liste et en comparant x à chaque élément de l'ensemble ens.
- L'ajout d'un élément x à un ensemble ens peut se faire de deux manières:
- ajouter l'élément x n'importe où dans la liste (cela dépend de la représentation choisie pour la liste) sans faire de test de redondance,
- ajouter l'élément x n'importe où dans la liste (même remarque) en testant son éventuelle existence. Cela simplifiera ensuite la suppression et la recherche de l'élément.
- La suppression d'un élément x d'un ensemble ens peut se faire aussi de deux manières dépendantes du choix fait pour l'ajout, soit:
- Dans le premier cas, il faut parcourir toute la liste pour être sûr d'avoir supprimé toutes les occurrences de l'élément x.
- Dans le deuxième cas, on peut s'arrêter dès que l'on a trouvé l'élément x.
- L'énumération d'un ensemble se fait aussi en parcourant séquentiellement toute la liste.
Dans le cas d'un multi-ensemble:
- le test d'appartenance de l'élément x à l'ensemble ens est inchangé.
- L'adjonction de l'élément x se fera naturellement sans test d'existence de x.
- La suppression de l'élément x s'arrête à la première occurrence de l'élément x rencontrée.
- Pour l'énumération il faut parcourir là aussi toute la liste. Si le nombre d'occurrences des éléments est important, il faut alors utiliser une liste de couple < x, nboccurrences(x)>. On adapte alors l'ajout, la suppression et la recherche à cette nouvelle représentation.
Représentation statique
Le tableau que l'on va utiliser doit être surdimensionné. Pour connaître le nombre exact d'élément actuellement dans l'ensemble, il est nécessaire d'utiliser un indicateur de position du dernier élément de l'ensemble dans le tableau (leur nombre), ce qui donne:
Constantes
Nbmax = 20
Types
t_element = ... /* Définition du type des éléments */ t_vectNbmaxelts = Nbmax t_element /* Définition du tableau des éléments */ t_ensemble = enregistrement /* Définition du type t_ensemble */ t_vectNbmaxelts elts entier nb fin enregistrement t_ensemble
Variable
t_ensemble ens
En utilisant cette déclaration, les algorithmes des différentes opérations sur les ensembles sont les suivants:
Appartenance de x à l'ensemble ens:
algorithme fonction appartient : booléen Paramètres locaux élément x ensemble ens Variables élément i Début i1 tant que (i <= ens.nb) et (x <> ens.elts[i]) faire i
i + 1 fin tant que retourne (i <= ens.nb) fin algorithme fonction appartient
Remarque: On peut éviter le test de dépassement (i <= ens.nb) en positionnant une sentinelle (l'élément x recherché) à la place ens.nb+1. De cette façon le test de boucle ne porte que sur l'égalité de l'élément à x. Si on sort de la boucle à l'indice ens.nb+1 c'est que x n'appartient pas à l'ensemble ens.
Dans ce cas, l'algorithme devient:
algorithme fonction appartient : booléen Paramètres locaux élément x ensemble ens Variables élément i Début i1 ens.elts[ens.nb+1]
x tant que (x <> ens.elts[i]) faire i
i + 1 fin tant que retourne (i = ens.nb + 1) fin algorithme fonction appartient
Ajout de x à l'ensemble ens avec test d'existence:
algorithme procédure ajoute_test_avec
Paramètres locaux
élément x
Paramètres globaux
ensemble ens
Début
si non(appartient(x,ens)) alors
ens.nb 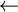 ens.nb + 1
ens.elts[ens.nb]
ens.nb + 1
ens.elts[ens.nb] 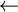 x
fin si
fin algorithme procédure ajoute_test_avec
x
fin si
fin algorithme procédure ajoute_test_avec
Dans ce cas, la suppression de x de l'ensemble ens est simple et correspond à l'algorithme suivant:
algorithme procédure supprimer_test_avec Paramètres locaux élément x Paramètres globaux ensemble ens Variables élément i Début i1 tant que (i <= ens.nb) et (x <> ens.elts[i]) faire i
i + 1 fin tant que si x = ens.elts[i] alors ens.elts[i]
ens.elts[ens.nb] ens.nb
ens.nb - 1 fin si fin algorithme procédure supprimer_test_avec
Remarque: Là aussi, x pourrait être utilisé comme sentinelle.
Ajout de x à l'ensemble ens sans test d'existence:
algorithme procédure ajoute_test_sans Paramètres locaux élément x Paramètres globaux ensemble ens Début ens.nbens.nb + 1 ens.elts[ens.nb]
x fin algorithme procédure ajoute_test_sans
Dans ce cas, la suppression de x de l'ensemble ens doit parcourir toute la liste pour y supprimer toutes les occurrences de x, ce correspond à l'algorithme suivant:
algorithme procédure supprimer_test_sans Paramètres locaux élément x Paramètres globaux ensemble ens Variables élément i Début i1 tant que (i <= ens.nb) faire si x <> ens.elts[i] alors i
i + 1 sinon ens.elts[i]
ens.elts[ens.nb] ens.nb
ens.nb - 1 fin si fin tant que fin algorithme procédure supprimer_test_sans
Remarques générales:
- L'ensemble vide est testé par ens.nb = 0, il suffit donc d'affecter à ens.nb la valeur 0 pour correspondre à l'opération abstraite ensemblevide.
- Dans le cas des multi-ensemble:
- on peut conserver cette structure, mais il faut dans ce cas utiliser ajouter_test_sans et supprimer_test_avec pour gérer les occurrences multiples.
- On peut aussi utiliser une liste de couple < x, nboccurrences(x)> où chaque élément apparaît plusieurs fois. Dans ce cas, l'ajout devra créer le couple s'il n'existe pas ou ajouter 1 au nombre d'occurrences s'il existe déjà. De même pour la suppression, on se contentera de diminuer le nombre d'occurrences de 1 et de supprimer vraiment l'élément si ce nombre atteint 0.
Représentation dynamique
Il est quelquefois difficile, voir impossible, de déterminer le nombre maximum d'éléments de l'ensemble. Dans ce cas, une représentation statique (sous forme de tableau) est peu envisageable et la solution qui s'impose est alors la représentation dynamique (sous forme de liste chaînée). Dans ce cas, la définition du type ensemble est la suivante:
Types
t_element = ... /* Définition du type des éléments */ t_pensemble =t_ensemble /* Définition du pointeur sur enregistrement */ t_ensemble = enregistrement /* Définition du type t_ensemble */ t_element elt t_pensemble suivant fin enregistrement t_ensemble
Variable
t_pensemble ens
En utilisant cette déclaration, les algorithmes des différentes opérations sur les ensembles sont les suivantes:
Appartenance de x à l'ensemble ens:
algorithme fonction appartient : booléen Paramètres locaux élément x t_pensemble ens Variables t_pensemble pens Début pensens tant que (pens <> NUL) et (x <> pens
.elt) faire pens
pens
.suivant fin tant que retourne (pens <> NUL) fin algorithme fonction appartient
Remarque: Avec cette représentation, l'emploi d'une sentinelle exige un lien directement sur le dernier élément. Dans le cas contraire, il faudrait d'abord parcourir la liste d'éléments pour positionner la sentinelle, ce qui serait trop coûteux.
Ajout de x à l'ensemble ens avec test d'existence:
algorithme procédure ajoute_test_avec
Paramètres locaux
élément x
Paramètres globaux
t_pensemble ens
Variables
t_pensemble pens
Début
si non(appartient(x,ens)) alors
allouer(pens)
pens .elt
.elt  x
si ens = NUL alors /* Cas particulier de l'ensemble vide */
pens
x
si ens = NUL alors /* Cas particulier de l'ensemble vide */
pens .suivant
.suivant  NUL /* Pas de suivant */
sinon
pens
NUL /* Pas de suivant */
sinon
pens .suivant
.suivant  ens /* Création de l'élément en 1ère place */
fin si
ens
ens /* Création de l'élément en 1ère place */
fin si
ens  pens
fin si
fin algorithme procédure ajoute_test_avec
pens
fin si
fin algorithme procédure ajoute_test_avec
Remarque: On pourrait en cas de non existence de l'élément x l'ajouter en fin de liste puisque sa recherche nous conduit à la fin de la liste.
Dans ce cas, la suppression de x de l'ensemble ens est simple et correspond à l'algorithme suivant:
algorithme procédure supprimer_test_avec Paramètres locaux élément x Paramètres globaux t_pensemble ens Variables t_pensemble pens, tpens Début pensens tant que (pens <> NUL) et (x <> pens
.elt) faire tpens
pens /* Mémorisation du précédent */ pens
pens
.suivant fin tant que si x = pens
.elt alors si pens <> ens alors /* Modification du lien de succession */ tpens
.suivant
pens
.suivant sinon /* cas particulier du premier élément */ ens
ens
.suivant fin si libérer(pens) /* suppression de l'élément */ fin si fin algorithme procédure supprimer_test_avec
Ajout de x à l'ensemble ens sans test d'existence:
algorithme procédure ajoute_test_sans Paramètres locaux élément x Paramètres globaux t_pensemble ens Variables t_pensemble pens Début allouer(pens) pens.elt
x si ens = NUL alors /* Cas particulier de l'ensemble vide */ pens
.suivant
NUL /* Pas de suivant */ sinon pens
.suivant
ens /* Création de l'élément en 1ère place */ fin si ens
pens fin algorithme procédure ajoute_test_sans
Dans ce cas, la suppression de x de l'ensemble ens doit, là encore, parcourir toute la liste pour y supprimer toutes les occurrences de x, ce correspond à l'algorithme suivant:
algorithme procédure supprimer_test_sans Paramètres locaux élément x Paramètres globaux t_pensemble ens Variables t_pensemble pens, tpens Début pensens tant que (pens <> NUL) faire si x = pens
.elt alors si pens <> ens alors /* Modification du lien de succession */ tpens
.suivant
pens
.suivant sinon /* cas particulier du premier élément */ ens
ens
.suivant fin si libérer(pens) /* suppression de l'élément */ fin si tpens
pens /* Mémorisation du précédent */ pens
pens
.suivant fin tant que fin algorithme procédure supprimer_test_sans
Conclusion
Dans tous les cas considérés il y a toujours au moins une opération dont la complexité est au pire et en moyenne O(N) ou N est soit le nombre d'éléments présents, soit le nombre d'éléments possibles dans l'ensemble. Ce qui signifie qu'au delà d'une centaine d'éléments ces méthodes ne sont plus envisageables.