Epita:Algo:Cours:Info-Spe:les graphes
Sommaire |
Généralités
Il existe deux sortes de graphes, les graphes non orientés (undirected graphs), pour lesquels les relations, symétriques, sont appelées arêtes (figure 1) et les graphes orientés (directed graphs) pour lesquels les relations, non symétriques, sont appelées arcs (figure 2).
Dans l'exemple suivant (figure 1), les sommets sont des villes et les relations entre ces sommets symbolisent l’existence d’une liaison aérienne. On prend pour principe que s’il y a un vol aller, il y a un vol retour. Le graphe est non orienté et si deux sommets sont en relation, on dit alors qu’il existe une arête entre ces deux sommets. Par exemple, il existe une arête {Lyon, Strasbourg}. Les questions auxquelles on peut répondre dans ce cas sont : Peut on aller de Marseille à Brest ? (Franchement, quelle idée, être à Marseille et vouloir aller à Brest). Enfin admettons... Et dans ce cas, quel est le chemin qui nécessite le moins d’escales ?
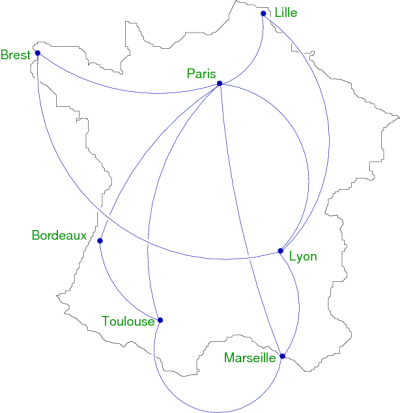
|
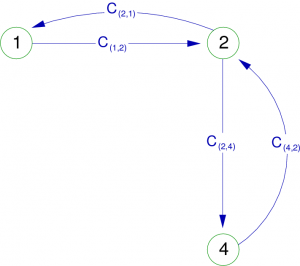
Pour l’exemple suivant (figure 2), nous avons la représentation d’un organigramme (un diagramme des flux, ça fait toujours bien dans les cocktails) qui détermine la valeur de la factorielle de n. Dans ce cas, les sommets sont des blocs d’instructions, et les relations ne symbolisent pas seulement le passage d’un bloc à l’autre. En effet, elles en définissent aussi le sens. Par exemple, on peut passer du sommet S2 au sommet S3, mais pas l’inverse. On dit dans ce cas que le graphe est orienté et l’existence d’une relation entre deux sommets est appelée arc. Par exemple, il existe un arc (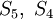 ).
).

|
Définitions et terminologies
Les graphes orientés
Les p-graphes
Les p-graphes sont la forme la plus courante des graphes orientés (directed graphs ou digraphs). Un p-graphe est défini par un couple < S, A >, où :
- S est un ensemble fini de sommets (vertex, vertices) appelés aussi noeuds (node) dans certains cas. Le nombre de sommets de G est appelé ordre de G. On utilise par convention la lettre N pour désigner l'ordre de G.
- A est une famille (ensemble avec redondances autorisées) de paires ordonnées de sommets appelées arcs (arcs or directed edges). On utilise par convention la lettre M pour désigner le nombre d'arcs de G.
- Un p-graphe peut-être valué ou pondéré (weighted). il est alors défini par un triplet < S, A, C > où C est une fonction de A sur
 appelée fonction de coût. On utilise par convention Cu pour représenter le coûts, le poids ou la valeur d'un arc u.
appelée fonction de coût. On utilise par convention Cu pour représenter le coûts, le poids ou la valeur d'un arc u.
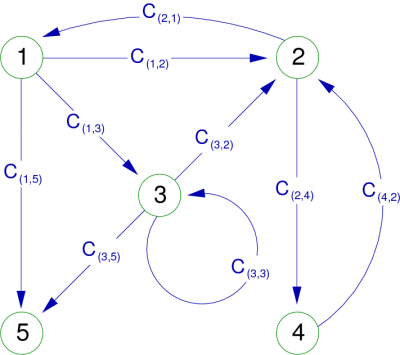
Lorsque les graphes sont petits (peu de sommets et de relations entre ces sommets), on peut les représenter sous la forme suivante appelée diagramme sagittal :
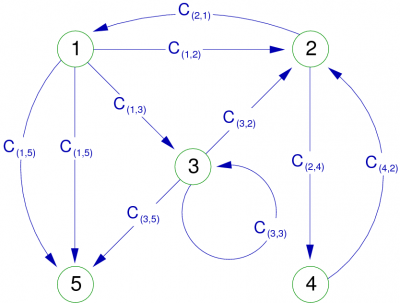
|
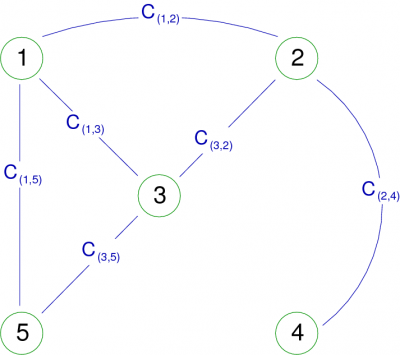
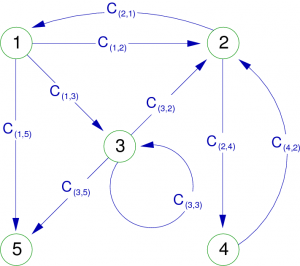
L'exemple de la figure 3 montre un 2-graphe d'ordre 5. Il y a en effet deux arcs (1,5) et 5 sommets. Cet exemple montre aussi une boucle (loop), c'est à dire un arc reliant un sommet avec lui-même (en l'occurrence le sommet 3).
Remarque : Un graphe orienté peut parfois être traité de manière non orientée quand la nature du problème l’impose. Le métro Parisien, par exemple, est de nature orienté (dû à quelques stations) et pourtant, pour une recherche d’itinéraire, nous avons tout intérêt à le considérer comme non orienté.
Les graphes orientés n’échappant pas à la règle, voici les différents termes qui les caractérisent :
- Un arc u de la forme (x,y) et noté u=x
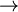 y a deux extrémités (end-points) telles que :
y a deux extrémités (end-points) telles que :
- x est l’extrémité initiale de l’arc u
- y est l’extrémité terminale de l’arc u
- y est le successeur de x
- x est le prédécesseur de y
- Deux arcs d’un graphe orienté sont dits adjacents s’ils ont au moins une extrémité commune.
- Dans un graphe orienté, le sommet y est dit adjacent (voisin) à x s’il existe un arc x
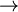 y.
y.
Remarque : L'ensemble des successeurs de x est noté Γ(x) (grand gamma de x), et celui des prédecesseurs Γ − 1(x).
- Un graphe orienté est dit complet si, pour tout couple de sommets (x,y), il existe un arc x
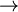 y.
y.
- Dans un graphe orienté, si un sommet x est l’extrémité initiale d’un arc u=x
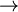 y, on dit que l’arc u est incident à x vers l’extérieur.
y, on dit que l’arc u est incident à x vers l’extérieur.
- On appelle le nombre d’arcs ayant x pour extrémité initiale le demi-degré extérieur (out-degree) de x et on le note
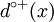 . On note l'ensemble des arcs incidents à x extérieurement ω + (x) (oméga plus de x) avec
. On note l'ensemble des arcs incidents à x extérieurement ω + (x) (oméga plus de x) avec 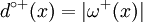 .
.
- Dans un graphe orienté, si un sommet x est l’extrémité terminale d’un arc u=y
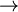 x, on dit que l’arc u est incident à x vers l’intérieur.
x, on dit que l’arc u est incident à x vers l’intérieur.
- On appelle le nombre d’arcs ayant x pour extrémité terminale le demi-degré intérieur (in-degree) de x et on le note
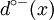 . On note l'ensemble des arcs incidents à x intérieurement ω − (x) (oméga moins de x) avec
. On note l'ensemble des arcs incidents à x intérieurement ω − (x) (oméga moins de x) avec 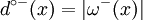 .
.
- Dans un graphe orienté, on appelle degré (degree) d'un sommet x le nombre d'arcs dont x est une extrémité. On le note
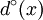 et on a
et on a 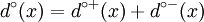 (le degré est égal à la somme des demi-degrés). L'ensemble des arcs incidents à x (dont x est une extrémité) est noté
(le degré est égal à la somme des demi-degrés). L'ensemble des arcs incidents à x (dont x est une extrémité) est noté 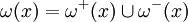 , avec évidemment
, avec évidemment 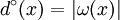 ..
..
Remarques :
- Les boucles sont comptées deux fois dans le degré
- Un sommet isolé est un sommet de degré nul
- Quand il y a ambiguïté, on peut préciser le nom du graphe en indice, par exemple :
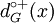 , ou
, ou 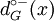 , etc.
, etc.
Un petit exemple pour conclure, sur le graphe de la figure 3, on a pour le sommet 2 :
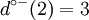
|
ω − (2) = {(1,2),(3,2),(4,2)} | Γ − 1(2) = {1,3,4} |
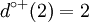
|
ω + (2) = {(2,1),(2,4) | Γ(2) = {1,4} |
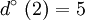
|
ω(2) = {(1,2),(2,1),(2,4),(3,2),(4,2)} |
Les 1-graphes
Il s'agit des p-graphes les plus simples avec p=1. Pour deux sommets distincts x et y il ne peut y avoir qu'un seul arc x  y. Le 2-graphe de la figure 3 pourrait éventuellement devenir le 1-graphe de la figure 4. On constate qu'un des deux arcs (1,5) a disparu.
y. Le 2-graphe de la figure 3 pourrait éventuellement devenir le 1-graphe de la figure 4. On constate qu'un des deux arcs (1,5) a disparu.
|
Dans un 1-graphe, chaque arc pouvant être représenté sans ambiguïté par un couple (x,y), la famille A devient un ensemble. De la même manière, on a | Γ(x) | = | ω + (x) | (l'ensemble des successeurs d'un sommet x est égal au nombre d'arcs incidents à x vers l'extérieur). Il en va de même pour la précédence, et l'on a là aussi | Γ − 1(x) | = | ω − (x) | .
On considère souvent 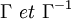 comme des applications multivoques parce qu'elles associent à tout sommet x de S un ensemble de sommets de S.
Γ est alors appelée application-successeur et Γ − 1 application-prédécesseur. Pour le graphe de la figure 4, nous aurions par exemple pour chaque sommet :
comme des applications multivoques parce qu'elles associent à tout sommet x de S un ensemble de sommets de S.
Γ est alors appelée application-successeur et Γ − 1 application-prédécesseur. Pour le graphe de la figure 4, nous aurions par exemple pour chaque sommet :
| Γ(1) = {2,3,5} |
| Γ(2) = {1,4} |
| Γ(3) = {2,3,5} |
| Γ(4) = {2} |
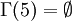
|
Dans ces conditions, on peut représenter le graphe G=< S,A > par G=< S,Γ> ou A est remplacé par l'application multivoque Γ (ce qui amène aux listes d'adjacences).
Remarque :
- Par la suite, nous utiliserons essentiellement des 1-graphes (graphes majoritairement implémentés) et le terme graphe désignera implicitement des 1-graphes.
- Pour les anglo-saxons, le terme graph désigne des graphes non orientés, l'expression digraph (directed graph) étant utilisée pour les graphes orientés.
Type abstrait "graphe orienté"
Le type graphe orienté utilise le type Sommet, nous allons donc donner sa définition abstraite.
types
sommet
utilise
entier
opérations
som : entiersommet n° : sommet
entier
axiomes
n°(som(i)) = i
avec
entier i
Remarque : Par la suite, sauf cas particulier, nous considérerons que les sommets sont des entiers.
Lors de l'utilisation des opérations abstraites sur les graphes orientés, nous admettrons les évidences suivantes :
- l'ajout d'un arc induit celui de ses sommets si ceux-ci n’appartiennent pas au graphe.
- la suppression d'un arc n'implique pas celle de ses sommets.
- la suppression d'un sommet induit celle de tous les arcs dont il est une extrémité.
- l'ajout d'un arc ou d'un sommet déjà présent ne fait rien.
Nous n’allons pas fournir la définition axiomatique complète des graphes orientés, mais seulement leur signature, à laquelle nous ajouterons quelques fonctions de manipulation complémentaires, pour pouvoir les utiliser dans les algorithmes abstraits que nous présenteront, ce qui donne :
types
graphe
utilise
sommet, entier, booléen
opérations
graphevide :graphe ajouterlesommet _ à _ : sommet x graphe
graphe ajouterlarc <_,_> à _ : sommet x sommet x graphe
graphe _ estunsommetde _ : sommet x graphe
booléen <_,_> estunarcde _ : sommet x sommet x graphe
booléen d°+ : sommet x graphe
entier ièmesucc : entier x sommet x graphe
sommet d°- : sommet x graphe
entier ièmepred : entier x sommet x graphe
sommet retirerlesommet _ de _ : sommet x graphe
graphe retirerlarc <_,_> de _ : sommet x sommet
graphe nbsommets : graphe
entier nbarcs : graphe
entier
extensions
premiersucc : sommet x graphesommet succsuivant : sommet x sommet x graphe
sommet
valuation
coût : sommet x sommet x grapheréel ajouterlarc <_,_> de coût _ à _ : sommet x sommet x réel x graphe
graphe
Les graphes non orientés
Dans certains cas, comme les liaisons aériennes, l'orientation des relations importe peu (on part du principe que s'il y a l'aller, il y a le retour). On ne s'intéresse alors qu'au fait que deux sommets soient reliés ou non entre eux.
Les multigraphes
Les multigraphes sont la forme la plus courante des graphes non orientés (undirected graphs). Un multigraphe est défini par un couple (S,A), où :
- S est un ensemble fini de sommets (vertex, vertices) appelés aussi noeuds (node) dans certains cas. Le nombre de sommets de G est appelé ordre de G. On utilise par convention la lettre N pour désigner l'ordre de G.
- A est une famille (ensemble avec redondances autorisées) de paires ordonnées de sommets appelées arêtes (edges or lines). On utilise par convention la lettre M pour désigner le nombre d'arêtes de G.
- Un multigraphe peut-être valué ou pondéré (weighted). il est alors défini par un triplet (S,A,C) où C est une fonction de A sur
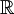 appelée fonction de coût. On utilise par convention Cu pour représenter le coûts, le poids ou la valeur d'une arête u.
appelée fonction de coût. On utilise par convention Cu pour représenter le coûts, le poids ou la valeur d'une arête u.
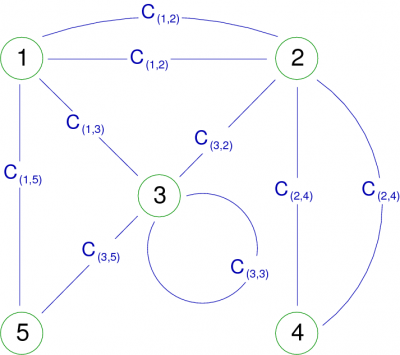
Lorsque les graphes sont petits (peu de sommets et de relations entre ces sommets), on peut les représenter sous la forme suivante appelée diagramme sagittal :
|
L'exemple de la figure 5 montre un multigraphe d'ordre 5. Il y a en effet deux arêtes {1,2}, deux arêtes {2,4} et 5 sommets. Cet exemple montre aussi une boucle (loop), c'est à dire une arête reliant un sommet avec lui-même (en l'occurrence le sommet 3).
Les graphes non orientés n’échappant pas à la règle, voici les différents termes qui les caractérisent :
- Une arête u de la forme {x,y} et noté u=x − y a deux extrémités (end-points) x et y. Par analogie avec les graphes orientés, on dit parfois que y est le successeur de x, que y est le prédecesseur de x et inversement.
- Deux arêtes d'un graphe non orienté sont dits adjacentes si elles ont au moins une extrémité commune.
- Dans un graphe non orienté, les sommets x et y sont dits adjacents (voisins) s’il existe une arête x − y.
Remarque : Comme il n'y a plus d'orientation, on ne parle plus de successeurs ou de prédecesseurs, mais seulement de voisins. L'ensemble des voisins de x est noté Γ(x) (grand gamma de x).
- Un graphe non orienté est dit complet si, pour tout couple de sommets (x,y), il existe une arête x − y.
- Dans un graphe non orienté, on appelle degré (degree) d'un sommet x le nombre d'arêtes dont x est une extrémité. On le note
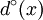 . L'ensemble des arêtes dont x est une extrémité est noté ω(x), avec évidemment
. L'ensemble des arêtes dont x est une extrémité est noté ω(x), avec évidemment 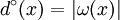 .
.
Remarques :
- Un sommet isolé est un sommet de degré nul
- Quand il y a ambiguïté, on peut préciser le nom du graphe en indice, par exemple :
Un petit exemple pour conclure, sur le graphe de la figure 5, on a pour chaque sommet :
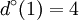
|
ω(1) = {{1,2},{1,2},{1,3},{1,5}} | Γ(1) = {1,3,5} |
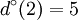
|
ω(2) = {{2,1},{2,1},{2,3},{2,4},{2,4}} | Γ(2) = {1,3,4} |
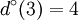
|
ω(3) = {{3,1},{3,2},{3,3},{3,5}} | Γ(3) = {1,2,3,5} |
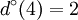
|
ω(4) = {{4,2},{4,2}} | Γ(4) = {2} |
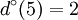
|
ω(5) = {{5,1},{5,3}} | Γ(5) = {1,3} |
Les graphes simples
Il s'agit des multigraphes les plus simples avec pour deux sommets distincts x et y une seule arête x − y. L'intérêt dans ce cas n'est pas de savoir combien d'arêtes relient deux sommets, mais simplement de savoir s'il y a relation entre ces deux sommets. On ne retient alors qu'une arête entre deux mêmes sommets et on ignore les boucles. Le multigraphe de la figure 5 pourrait éventuellement devenir le graphe simple de la figure 6. On constate que les arêtes multiples (1,2), (4,2) et la boucle (3,3) ont disparu.
|
Remarque : un graphe simple est donc l'équivalent non orienté et sans boucle d'un 1-graphe.
On considère souvent Γ comme une application multivoque parce qu'elle associe à tout sommet x de S un ensemble de sommets de S. Γ est alors appelée application-voisin.
Dans ces conditions, on peut représenter le graphe G=< S,A > par G=< S,Γ> ou A est remplacé par l'application multivoque Γ (ce qui amène aux listes d'adjacences).
Remarque :
- Par la suite, nous utiliserons essentiellement des graphes simples (graphes majoritairement implémentés) et le terme graphe non orienté désignera implicitement des graphes simples.
Type abstrait "graphe non orienté"
Le type graphe non orienté utilise le type Sommet, nous allons donc donner sa définition abstraite.
types
sommet
utilise
entier
opérations
som : entiersommet n° : sommet
entier
axiomes
n°(som(i)) = i
avec
entier i
Remarque : Par la suite, sauf cas particulier, nous considérerons que les sommets sont des entiers.
Lors de l'utilisation des opérations abstraites sur les graphes non orientés, nous admettrons les évidences suivantes :
- l'ajout d'une arête induit celui de ses sommets si ceux-ci n’appartiennent pas au graphe.
- la suppression d'une arête n'implique pas celle de ses sommets.
- la suppression d'un sommet induit celle de toutes les arêtes dont il est une extrémité.
- l'ajout d'une arête ou d'un sommet déjà présent ne fait rien.
Nous n’allons pas fournir la définition axiomatique complète des graphes non orientés, mais seulement leur signature, à laquelle nous ajouterons quelques fonctions de manipulation complémentaires, pour pouvoir les utiliser dans les algorithmes abstraits que nous présenteront, ce qui donne :
types
graphe
utilise
sommet, entier, booléen
opérations
graphevide :graphe ajouterlesommet _ à _ : sommet x graphe
graphe ajouterlarête <_,_> à _ : sommet x sommet x graphe
graphe _ estunsommetde _ : sommet x graphe
booléen <_,_> estunearêtede _ : sommet x sommet x graphe
booléen d° : sommet x graphe
entier ièmevoisin : entier x sommet x graphe
sommet retirerlesommet _ de _ : sommet x graphe
graphe retirerlarête <_,_> de _ : sommet x sommet
graphe nbsommets : graphe
entier nbarêtes : graphe
entier
extensions
premiervoisin : sommet x graphesommet voisinsuivant : sommet x sommet x graphe
sommet
valuation
coût : sommet x sommet x grapheréel ajouterlarête <_,_> de coût _ à _ : sommet x sommet x réel x graphe
graphe
Les parties de graphe
Les sous-graphes
Soit G=< S, A > un graphe orienté (ou non). Le sous-graphe (subgraph) de G engendré par S’ 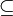 S est le graphe G’=< S’, A > dont les sommets sont les éléments de S’ et dont les arcs (arêtes) sont ceux de
S est le graphe G’=< S’, A > dont les sommets sont les éléments de S’ et dont les arcs (arêtes) sont ceux de 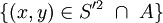 , c'est à dire ceux ayant leurs deux extrémités dans S’.
, c'est à dire ceux ayant leurs deux extrémités dans S’.
Ce qui pour un graphe orienté pourrait donner :
| graphe G | graphe G' |
|
|
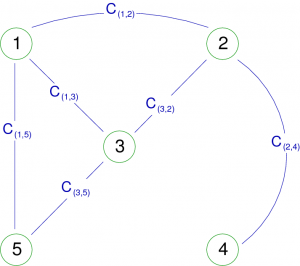
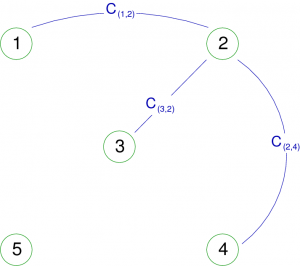
Les graphes partiels
Soit G=< S, A > un graphe orienté (ou non), le graphe partiel de G engendré par A’ 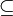 A est le graphe G’=< S, A’ > dont les sommets sont les éléments de S et dont les arcs (arêtes) sont ceux de A’.
A est le graphe G’=< S, A’ > dont les sommets sont les éléments de S et dont les arcs (arêtes) sont ceux de A’.
Ce qui pour un graphe non orienté pourrait donner (on notera le sommet 5 isolé) :
| graphe G | graphe G' |
|
|
Remarque : Lorsque l'on supprime d'un graphe et des sommets et des arcs, on parle parfois de sous graphe partiel.
Chemins et connexités
Définitions
- Dans un graphe orienté G, on appelle chemin (path) de longueur λ une suite de (λ + 1) sommets (S0,S1,...,Sλ) tels que
![\forall i \in [0,\lambda-1], S_i\rightarrow S_{i+1}](https://algo.infoprepa.epita.fr/images/math/c/4/5/c45b024202484d31669279dd75b7481e.png) est un arc de G.
est un arc de G.
- Dans un graphe non orienté G, on appelle chaîne (chain) de longueur λ une suite de (λ + 1) sommets (S0,S1,...,Sλ) tels que
![\forall i \in [0,\lambda-1], S_i\rightarrow S_{i+1}](https://algo.infoprepa.epita.fr/images/math/c/4/5/c45b024202484d31669279dd75b7481e.png) est une arête de G.
est une arête de G.
- On considère que tout chemin (chaîne) d’un sommet vers lui-même est de longueur 0.
- Un chemin (une chaîne) est dit élémentaire s’il ne contient pas plusieurs fois le même sommet.
- Dans un graphe orienté (non orienté), un chemin (une chaîne) (S0,S1,...,Sλ dont les λ) arcs (arêtes) sont tous distincts deux à deux et tel que les deux sommets aux extrémités sont les mêmes est appelé circuit (cycle).
- Un graphe orienté est dit fortement connexe (stongly connected) si pour toute paire ordonnée de sommets distincts (x,y), il existe un chemin de x vers y.
- Un graphe non orienté est dit connexe (connected) si pour toute paire de sommets distincts {x,y}, il existe un chaîne reliant x et y.
- On appelle composante fortement connexe (strongly connected components) d’un graphe orienté, un sous-graphe fortement connexe maximal. C'est à dire un sous-graphe fortement connexe qui n’est pas inclus dans un autre sous-graphe fortement connexe.
- On appelle composante connexe (connected components) d’un graphe non orienté, un sous-graphe connexe maximal. C'est à dire un sous-graphe connexe qui n’est pas inclus dans un autre sous-graphe connexe.
Représentation des graphes
Il existe plusieurs façons de représenter les graphes. Le choix de la méthode de représentation dépend de plusieurs critères dont le coté évolutif ou statique du graphe. Nous allons donc envisager trois formes de représentation :
- Les matrices (pour un ensemble S complètement statique)
- Les listes statique-dynamique (pour un ensemble S complètement statique)
- Les listes dynamiques (pour un ensemble S évolutif).
Représentation sous forme de matrice
Si l’ensemble S n’évolue jamais, il est possible d’utiliser des matrices carrées n x n de booléens appelées Matrices d’adjacences ( n représentant le nombre de sommets du graphe). Nous avons alors la déclaration de types suivante :
Constantes
Nbsommet = 4
Types
t_graphe = Nbsommet x Nbsommet booleen /* Définition de la matrice représentant le graphe */
Variable
t_graphe g
L’élément g[x,y] est vrai s’il existe une relation entre le sommet x et le sommet y. Sur la Figure 9, nous pouvons voir un exemple de graphe orienté, et sa représentation sous forme de matrice de booléen.
remarque : Afin de clarifier la lecture, seuls les arcs existants sont mentionnés (Vrai).
| graphe G | Matrice d'adjacence de G |
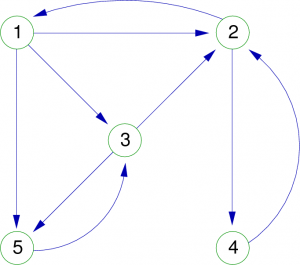
|
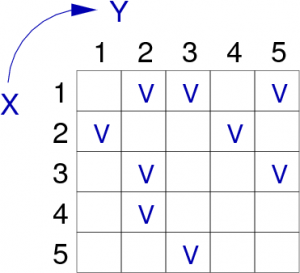
|
Bien entendu, si le graphe est valué il n’est plus possible de se contenter d’une matrice de booléen. Dans ce cas, la matrice devient : soit une matrice de coûts de types simples (entier, réel, etc.) si l’on n’utilise pas l’intégralité du domaine de définition de ces types et qu’une valeur peut être utilisée pour signaler l’absence d’arc ou d'arête, soit une matrice de coûts définis par l’utilisateur contenant les valeurs plus un booléen. Nous retiendrons la solution générique avec le booléen, ce qui donnerait pour un graphe valué par des éléments la déclaration suivante :
Constantes
Nbsommet = 4
Types
t_cout = ... /* Définition du type du coût */ t_relation = enregistrement /* Définition du type t_relation (arc ou arête) */ t_cout cout booleen existe fin enregistrement t_relation
t_graphe = Nbsommet x Nbsommet t_relation /* Définition de la matrice représentant le graphe */
Variable
t_graphe g
Il existe une relation entre deux sommets i et j si l’élément G[i,j].relation est Vrai. Sur la Figure 10, nous pouvons voir un exemple de graphe orienté valué, et sa représentation sous forme de matrice d’adjacence dont les éléments sont constitués d'un entier et d'un booléen indiquant si la relation (arc ou arête) existe entre les deux sommets concernés.
| graphe G valué | Matrice d'adjacence de G |
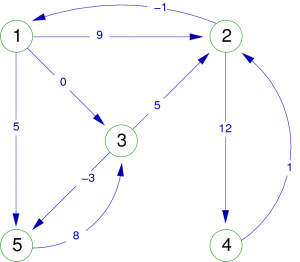
|
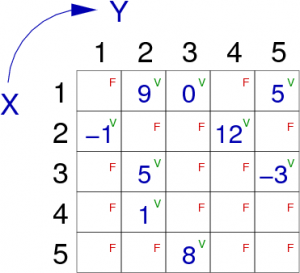
|
Remarque : L’ensemble S dans certains cas particuliers pourrait légèrement évoluer. Pour gérer cette possibilité, il sera nécessaire de surdimensionner la matrice au départ.
La représentation matricielle est très pratique pour tester l’existence d’un arc. Il est facile d’ajouter ou de supprimer un arc (il suffit de basculer le champ existe à Vrai ou à Faux selon le cas). Il est tout aussi facile de parcourir tous les successeurs ou prédécesseurs d’un sommet et donc de déterminer son degré ou ses demi-degrés.
L'algorithme de la fonction dde déterminant le demi-degré extérieur d'un sommet x pourrait être :
Algorithme fonction dde : entier Paramètres locaux t_graphe g /* g est le graphe */ entier x /* x est un sommet de g */ Variables entier d /* d est le dde temporaire */ entier y /* y est un sommet de g */ Début d0 /* initialisation de d */ pour y
1 jusqu'à Nbsommet faire si g[x,y].existe alors /* il existe une relation entre x et y */ d
d + 1 /* un successeur de plus */ fin si fin pour retourne(d) /* retourne le nombre de successeurs de x */ Fin algorithme fonction dde
Remarque : Il suffit pour le demi-degré intérieur de x, de reprendre le même algorithme et de simplement tester G[y,x].existe.
Malheureusement, un parcours complet exige un temps d’ordre Nbsommet2 et le stockage du graphe un espace mémoire du même ordre. Pour régler ces différents problèmes, nous utiliserons une autre forme de représentation appelée Liste d’adjacence.
Représentation sous forme de Liste
Cette représentation peut revêtir plusieurs formes (Ca lui fait un Look ?!). En fait, cela dépend de S. Si celui-ci est statique, nous aurons alors un tableau représentant les sommets, auquel sera associé pour chaque sommet une liste dynamique représentant les successeurs. Dans le cas où S est évolutif, le tableau sera remplacé par une liste dynamique.
Ensemble de sommets statique
Dans ce cas, la déclaration de la structure utilisée serait la suivante :
Constantes
Nbsommet = 4
Types
t_cout = ... /* Définition du type des coûts */ t_psomadj =t_somadj /* Définition du type pointeur sur sommet adjacent */ t_somadj = enregistrement /* Définition du type sommet adjacent */ entier numsomadj /* N° d'indice du sommet adjacent */ t_cout cout t_psomadj somadjsuiv /* pointeur sur sommet adjacent suivant */ fin enregistrement t_somadj t_graphe = Nbsommet t_psomadj /* Définition du type graphe (Vecteur représentant S) */
Variables
t_graphe g
Nous avons un graphe représenté par un vecteur de pointeurs sur une liste d'enregistrements correspondants aux sommmets adjacents. Chaque enregistrement contient le numéro du sommet adjacent sous forme d’entier (l'indice du vecteur et cet entier nous donne l'arc ou l'arête existante), un éventuel coût si le graphe est valué et un lien (symbolisé par la flèche) sur le sommet adjacent suivant ou NUL s'il n'y a pas d'autres successeurs au sommet (voir Figure 11).
| graphe G valué | Liste d'adjacence de G |

|
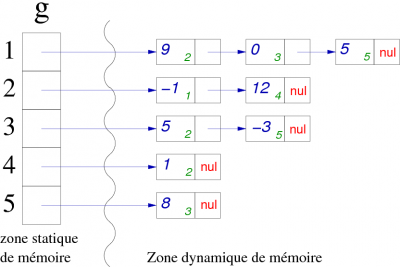
|
Attention : la liste associée à un sommet contient uniquement ses successeurs. Cette liste ne représente en aucun cas un chemin à partir du sommet (il n'existe pas de chemin (1,2,3), il n'y a pas d'arc (2,3)).
Si n est le nombre de sommets et p le nombre d’arcs, l’espace mémoire utilisé pour un graphe est d’ordre n + p (fois la taille évidemment). Pour un graphe non orienté, il serait de n + 2p (De là à penser, qu’une une arête vaut deux arcs, il n’y a qu’un pas que je ne franchirai pas). Ce qui est le cas aussi d’un graphe orienté pour lequel il serait nécessaire d’effectuer un traitement sur les prédécesseurs. En effet, cette représentation ne prend en compte que les successeurs, il suffit alors de posséder une autre liste chaînée pour les prédécesseurs, comme on peut le voir sur la figure 12 (basée sur le graphe de la figure 11).
| Figure 12. Exemple de listes d'adjacences (prédécesseur et successeur). |
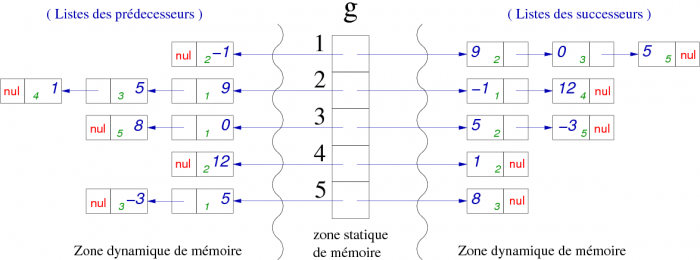
|
Dans ce cas, la déclaration de la structure utilisée serait la suivante :
Constantes
Nbsommet = 4
Types
t_element = ... /* Définition du type des elements */ t_cout = ... /* Définition du type des coûts */ t_psomadj =t_somadj /* Définition du type pointeur sur sommet adjacent */ t_sommet = enregistrement /* Définition du type sommet */ t_element elt t_psomadj premiersucc, premierpred fin enregistrement t_sommet
t_somadj = enregistrement /* Définition du type sommet adjacent */ entier numsomadj /* N° d'indice du sommet adjacent */ t_cout cout t_psomadj somadjsuiv /* pointeur sur sommet adjacent suivant */ fin enregistrement t_somadj
t_graphe = Nbsommet t_psommet /* Définition du type graphe (Vecteur représentant S) */
Variables
t_graphe g
On remarque que le vecteur ne contient pas juste un pointeur sur un sommet adjacent, mais deux (premier successeur et premier prédécesseur). Ayant besoin d'un enregistrement pour ces deux champs, on en profite pour rajouter une étiquette au sommet (un élément contenant des informations propres au sommet). Dans le cas du graphe de liaisons aériennes, cette étiquette pourrait contenir des informations propres aux villes comme leur latitude, leur longitude, leur altitude, etc...
Malheureusement, ces représentations (matrice ou liste) ne permettent pas de modéliser aisément un graphe dont l'ensemble des sommets serait évolutif.
Ensemble de sommets dynamique (évolutif)
D’autre part, si le graphe présente un ensemble de sommets évolutif, la représentation de ce dernier doit aussi se faire sous forme de liste chaînée. Dans ce cas, la déclaration de la structure utilisée serait la suivante :
Types
t_element = ... /* Définition du type des elements */ t_cout = ... /* Définition du type des coûts */
t_psommet =t_sommet /* Définition du type pointeur sur sommet */ t_psomadj =
t_somadj /* Définition du type pointeur sur sommet adjacent */
t_sommet = enregistrement /* Définition du type sommet */ t_element elt t_psommet somsuiv, somprec t_psomadj premiersucc, premierprec fin enregistrement t_sommet
t_somadj = enregistrement /* Définition du type sommet adjacent */ t_psommet somadj /* pointeur sur sommet adjacent */ t_cout cout t_psomadj somadjsuiv /* pointeur sur sommet adjacent suivant */ fin enregistrement t_somadj
t_graphe = t_psommet /* Définition du type graphe (pointeur sur un sommet) */
Variables
t_graphe g
Ce qui, toujours basé sur le graphe de la figure 11, donnerait le graphe de la figure 13 (Oh! C'est beau ...).
| Figure 13. Exemple de listes d'adjacences (prédécesseur et successeur) sommets non figés. |
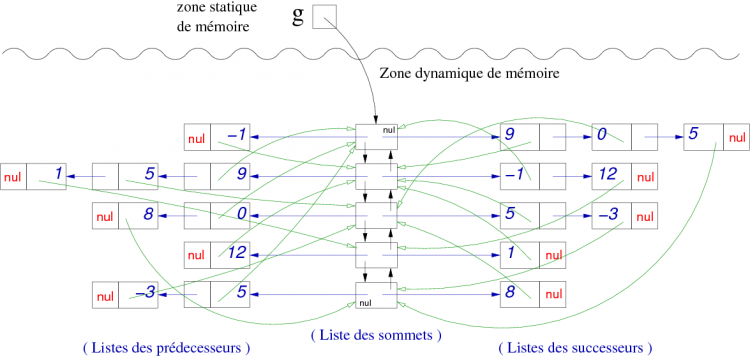
|
Remarques :
- La liste des sommets est doublement chaînée
- Avec une telle représentation, il devient facile de trouver un sommet adjacent, de calculer le demi-degré intérieur et extérieur d’un sommet, ainsi que de créer ou détruire des relations et des sommets.
- En revanche, ces facilités ne modifient pas le temps de recherche qui pour l’existence d’un arc, par exemple, peut être d’ordre n.
Parcours de Graphes
L’utilisation des graphes nécessite souvent l’étude exhaustive des sommets et arcs ou arêtes de celui-ci. Nous allons donc décrire les parcours (walk) de graphes. Ceux-ci se présentent sous deux formes qui sont, comme pour une arborescence, le parcours en profondeur et le parcours en largeur.
Parcours en profondeur
Ce parcours consiste à suivre, à partir d’un sommet donné, un chemin le plus loin possible. Puis à revenir en arrière pour explorer les chemins ignorés. Intrinsèquement, ce parcours est récursif. Le problème est de ne pas rentrer lors du parcours dans un circuit. Pour cela nous allons utiliser un tableau (vecteur) de marque qui nous permettra de savoir si nous sommes déjà passés par un sommet donné.
Graphe orienté
Considérons un graphe orienté dont les sommets sont non marqués. Nous choisissons un sommet S, nous le marquons. Nous prenons son premier successeur (s’il existe, évidemment…) puis nous recommençons à partir de celui-ci le même traitement que pour le sommet S. En fin de chemin (plus de successeur, damned !), nous revenons au sommet précédent et nous étudions son deuxième successeur, et ainsi de suite…
Malheureusement si le graphe n’est pas fortement connexe, il est probable que certains sommets n’aient pas été visités (marqués). Pour cela, nous plaçons une procédure itérative externe (parc_prof) qui vérifie que les sommets sont marqués. Si elle en trouve un qui ne l’est pas, elle rappelle la procédure de parcours (profondeur) à partir de ce dernier.
L’algorithme de parcours profondeur (version récursive) donne :
Algorithme procédure parc_prof Constantes Nbsommet = 4 Types t_vectNbool = Nbsommet booléen Variables t_vectNbool marque /* vecteur de marque */ t_graphe g entier x /* x est un sommet */ Début pour x1 jusqu’à Nbsommet faire /* Mise à "non marqué" des sommets */ marque[x]
faux fin pour pour x
1 jusqu’à Nbsommet faire /* Boucle principale */ si non(marque[x]) alors /* Si le sommet est "non marqué" */ profondeur(x,g,marque) /* => appel du parcours en profondeur */ fin si fin pour Fin Algorithme procédure parc_prof
Algorithme procédure profondeur Paramètres locaux entier x /* x est un sommet */ t_graphe g Paramètres globaux t_vectNbool marque /* vecteur de marque */ Variables entier i,y /* y est un sommet */ Début marque[x]vrai /* marquage du sommet x */ /* première rencontre de x */ pour i
1 jusqu’à d°+(x,g) faire y
i ème-succ-de x dans g /* rencontre à aller de l’arc(x,y) */ si non(marque[y]) alors profondeur(y,g,marque) /* appel récursif */ fin si /* rencontre au retour de l’arc(x,y) */ fin pour /* dernière rencontre de x */ Fin Algorithme procédure profondeur
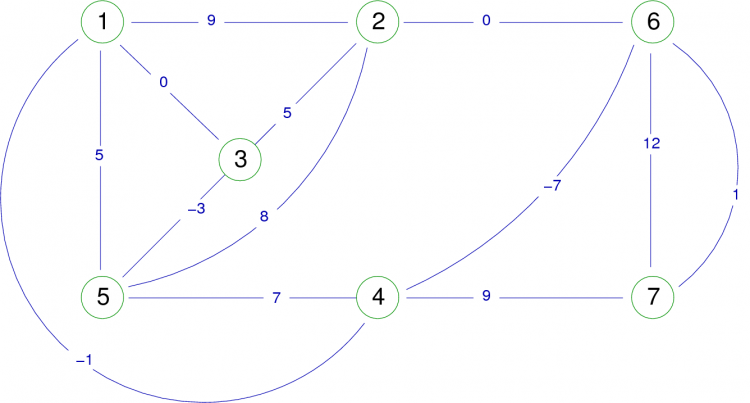
Prenons comme référence pour les exemples de parcours, le graphe suivant (figure 14).
| Figure 14. Graphe orienté valué. |
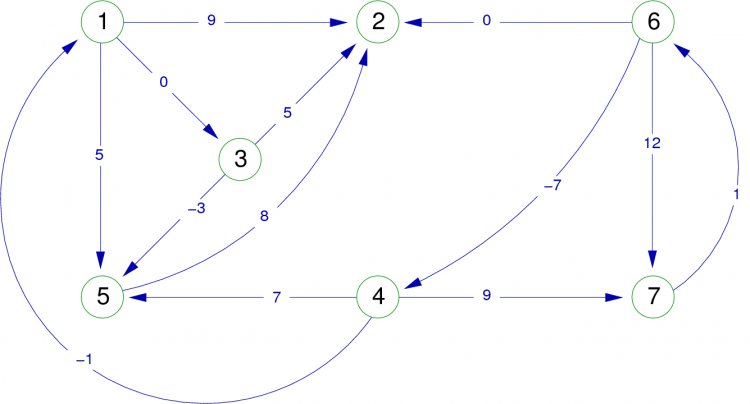
|
En supposant que l’ordre d’utilisation des sommets est croissant (pour les successeurs aussi), et que le sommet 1 est le premier choisi. Si l’on utilise le graphe orienté de la Figure 14 et que l’on insère dans l'algorithme un ordre d’écriture du sommet x lors de la première rencontre de celui-ci, nous obtenons l’affichage des sommets dans l'ordre suivant :
1, 2, 3, 5, 4, 7, 6
De la même manière, si l’ordre d’écriture est inséré lors de la dernière rencontre du sommet x, nous obtenons l’affichage des sommets dans l'ordre suivant :
2, 5, 3, 1, 6, 7, 4
Lors du parcours en profondeur d’un graphe orienté, si l'on dessine les arcs au fur et à mesure de leur rencontre, on obtient pour le graphe de la figure 14 la représentation graphique suivante (figure 15).
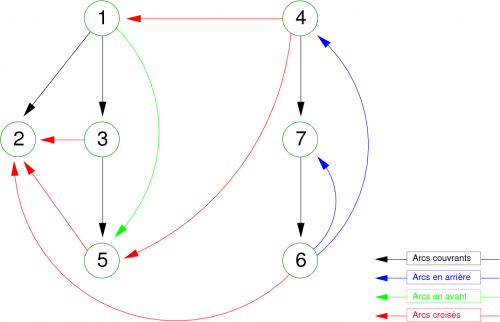
| Figure 15. Forêt couvrante associée au graphe de la figure 14. |
|
Sur cette représentation appelée forêt couvrante associée au parcours en profondeur du graphe g, on peut distinguer quatre sortes d’arcs :
- les arcs couvrants
- les arcs en arrière
- les arcs en avant
- les arcs croisés
Ils correspondent aux définitions suivantes :
- Les arcs (x,y) tels que hauteur(x) appelle hauteur(y) sont appelés arcs couvrants . Leur ensemble constitue une forêt couvrante de recherche en profondeur. Ce sont les arcs (1,2),(1,3),(3,5),(4,7) et (7,6) dans l’exemple donné figure 15.
- Les arcs (x,y) dont l’extrémité terminale est un ascendant de l’extrémité initiale dans la forêt couvrante sont appelés arcs en arrière. Ce sont les arcs (6,7) et (6,4) dans l’exemple donné figure 15.
- Les arcs (x,y) dont l’extrémité terminale est un descendant de l’extrémité initiale dans la forêt couvrante sont appelés arcs en avant. C'est l'arc (5,6) dans l’exemple donné figure 15.
- Les arcs (x,y) pour lesquels il n’existe pas de chemin entre leurs extrémités, dans la forêt couvrante, sont appelés arcs croisés. Ce sont les arcs (3,2),(5,2),(4,1),(4,5) et (6,2) dans l’exemple donné figure 15.
Remarques :
- Si par convention, on dessine les arcs de la forêt au fur et à mesure de leur rencontre et les différentes arborescences de la gauche vers la droite, les arcs croisés sont nécessairement dirigés de la droite vers la gauche.
- Certaines propriétés des forêts couvrantes associées aux parcours de graphe étant définie géographiquement, il est impératif de respecter la convention de représentation graphique évoquée dans la précédente remarque.
Si lors du parcours en profondeur du graphe, on affecte à chaque sommet x une valeur préfixe (pref(x)) qui correspond à son ordre de rencontre lors du parcours progondeur préfixe du graphe (première rencontre de x), on obtient les propriété suivantes :
- Si pref(x) < pref(y) alors l’arc (x,y) est un arc couvrant ou un arc en avant
- Si pref(x) > pref(y) alors l’arc (x,y) est un arc en arrière ou un arc croisé
Graphe non orienté
L’algorithme utilisé est le même que pour un graphe orienté. La complexité reste la même dans la mesure où l’on considérera pour un graphe ayant p arêtes qu’il possède 2p arcs (vous vous rappelez ?). Par contre, le sens du parcours oriente les arêtes et l’on parle encore d’arcs pour la forêt couvrante associée. Mais l’on ne distingue plus que deux types d’arcs :
- Les arcs couvrants : Ceux tels que hauteur(x)=(y)+1
- Les arcs en arrières : Ceux tels que x est un descendant de y dans la forêt couvrante.
Remarque :
- Si l’arête {x,y} est devenue un arc couvrant (lors du parcours), on ne doit pas la considérer quand on construit les arcs en arrière.
- Il n’y a pas d’arcs en avant puisque les arêtes sont non orientées.
- Il n’y a pas d’arcs croisés puisque deux sommets ne peuvent pas être adjacents sans être descendants l’un de l’autre (les relations sont symétriques).
Pour exemple, transformons le graphe orienté de la Figure 14 en graphe non orienté (Figure 16) :
| Figure 16. Graphe non orienté valué. |
|
Observons la forêt couvrante obtenue en figure 17 (Comme précédemment, les sommets sont traités en ordre numérique croissant et nous commençons par le sommet 1).
| Figure 17. Forêt couvrante associée au graphe de la figure 16. |
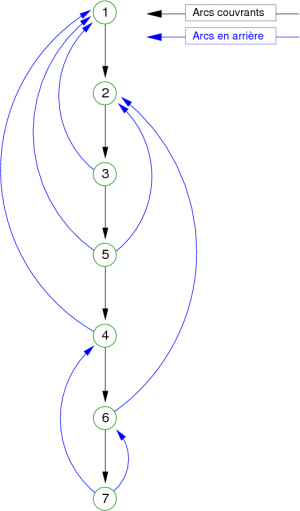
|
Remarque : Le graphe étant connexe, le parcours ne construit qu'une seule arborescence.
Parcours en largeur
Ce parcours consiste à suivre, à partir d’un sommet donné, tous les successeurs de celui-ci, puis à passer à tous les successeurs du 1er successeur, puis à tous les successeurs du 2ème , etc. Le parcours se fait, en fait, par distance (hauteur dans ce cas), c’est à dire que l’on parcourt d’abord tous les sommets se trouvant à une distance de 1 du sommet de départ, puis tous ceux qui se trouvent à une distance de 2 et ainsi de suite...
Remarque : Ce parcours aussi qualifié de hiérarchique est par nature itératif.
De la même façon que pour le parcours en profondeur, nous allons marquer les sommets parcourus, et si le graphe n’est pas fortement connexe, il est probable que certains sommets n’aient pas été visités (marqués). Pour cela, nous plaçons une procédure itérative externe qui vérifie que les sommets sont marqués. Si elle en trouve un qui ne l’est pas, elle rappelle la procédure de parcours à partir de ce dernier.
L’algorithme de parcours largeur (version itérative) utilise une File pour mémoriser les descendants directs de chaque sommet rencontré. Ce qui permet à la hauteur suivante de les récupérer dans l'ordre de rencontre; Cela donne l'algorithme suivant :
Algorithme procédure parc_larg Constantes Nbsommet = 4 Types t_vectNbool = Nbsommet booléen Variables t_vectNbool marque /* vecteur de marque */ t_graphe g entier x /* x est un sommet */ Début pour x1 jusqu’à Nbsommet faire /* Mise à "non marqué" des sommets */ marque[x]
faux fin pour pour x
1 jusqu’à Nbsommet faire /* Boucle principale */ si non(marque[x]) alors /* Si le sommet est "non marqué" */ largeur(x,g,marque) /* => appel du parcours en largeur */ fin si fin pour Fin Algorithme procédure parc_larg
Algorithme procédure largeur Paramètres locaux entier x /* x est un sommet */ t_graphe g Paramètres globaux t_vectNbool marque /* vecteur de marque */ Variables entier i,y,z /* y et z sont des sommets */ file f /* f stocke les descendants de x */ Début marque[x]vrai /* marquage du sommet de départ (x) */ f
filevide f
enfiler(f,x) /* stockage du sommet de départ (x) */ tant que non(estvide(f)) faire y
premier(f) /* récupération du 1er sommet stocké */ f
defiler(f) /* libérer la file de ce 1er sommet */ /* rencontre de y */ pour i
1 jusqu’à d°+(y,g) faire z
i ème-succ-de y dans g /* rencontre de l’arc(y,z) */ si non(marque[z]) alors marque[z]
vrai /* marquage du sommet descendant (z) */ f
enfiler(f,z) /* stockage du sommet descendant (z) */ fin si fin pour fin tant que Fin Algorithme procédure largeur
En supposant, encore une fois, que l’ordre d’utilisation des sommets soit croissant, et que le sommet 1 soit le premier choisi, si l’on utilise le graphe orienté de la Figure 14 et que l’on insère dans l'algorithme un ordre d’écriture du sommet y lors de la rencontre de celui-ci (y  premier(f)), nous obtenons l’affichage des sommets dans l'ordre suivant :
premier(f)), nous obtenons l’affichage des sommets dans l'ordre suivant :
1, 2, 3, 5, 4, 7, 6
Remarques :
- Sur cet exemple, l'ordre de rencontre des sommets est le même que pour le parcours profondeur préfixe. C'est absolument fortuit et du au fait que cet exemple (figure 14) est nul ;).
- La complexité est la même que pour le parcours en profondeur.
- Pour cet algorithme, le fait qu’il soit itératif rend extrêmement simple l’inclusion du programme principal dans la procédure largeur. Malgré cela, il est préférable de laisser les choses en l’état. En effet, vous pouvez désirer effectuer le parcours uniquement à partir d’un sommet sans vouloir parcourir l’intégralité du graphe, ce que l’inclusion ne permettrait plus.
(Christophe "krisboul" Boullay)