Epita:Algo:Cours:Info-Spe:Méthodes de hachage
Sommaire |
Principe du hachage
Soit E un ensemble de nom, supposons que la clé est le nom lui-même et que l'on associe à chaque élément x de l'ensemble E, un nombre h(x) compris entre 0 et 8 en procédant comme suit :
- Attribuons aux lettres a, b, c, ..., z leur valeur ordinale respective, soit 1, 2, 3, ..., 26
- Additionnons les valeurs des lettres
- Ajoutons au nombre obtenu le nombre de lettres composant la clé
- Calculons le modulo 9 de ce dernier pour obtenir h(x)
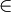 [0,8]
[0,8]
Pour l'ensemble E = { nathalie, caroline, arnaud, reda, mathieu, jerome, nicolas }, on obtient les valeurs de hachage suivantes :
|
|
Le tableau 1 montre le tableau de hachage associé à cet exemple. On peut constater que la restriction de h à E est injective et que l'on peut donc ranger chaque élément x de E dans l'élément d'indice h(x) du tableau.
Pour déterminer si un élément quelconque x appartient à E, il suffit alors de calculer l'indice v = h(x).
si v = 1 ou v = 7 alors
x n'appartient pas à E
sinon
on compare x avec l'élément y se trouvant en case v
si x = y alors
x appartient bien à E,
si' x 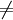 y alors
x n'appartient pas à E
y alors
x n'appartient pas à E
Remarque : Bien entendu, il est nécessaire de pouvoir reconnaître une case "vide" ou non.
Si l'on désire ajouter un élément x et que celui-ci présente une valeur de hachage déjà utilisée par un élément y, h n'est plus injective (x 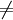 y et h(x) = h(y)) et l'on dit qu'il y a collision primaire entre x et y.
y et h(x) = h(y)) et l'on dit qu'il y a collision primaire entre x et y.
Nous verrons plus loin comment résoudre cette collision. Dans ce cas, la fonction donne accès à un petit groupe d'élément et non plus à un seul.
L'ensemble E a été "haché", d'où le nom de fonction de hachage.
On utilise les méthodes de hachage lorsque l'on doit classer les éléments d'une collection appartenant à un univers très grand. La taille de ce dernier nous empêche de le représenter en réservant une place mémoire par clé possible. On utilise alors une fonction de hachage h qui associe à chaque clé un entier compris entre 1 et m, où m est choisi en fonction de la taille prévue de la collection.
Pour toute clé x de la collection, h(x) (valeur de hachage primaire) donne l'indice de x dans le tableau de hachage. Cela nous permet de le rechercher, l'ajouter ou le supprimer. Le choix de la fonction de hachage est fondamental, celle-ci doit être :
- uniforme: c'est à dire que tous les éléments sont répartis le plus uniformément possible dans le tableau,
- facile et rapide à calculer : le but étant de ne pas affaiblir la méthode par un calcul long et fastidieux,
- Déterministe : renvoyer toujours le même résultat.
Il en résulte que la conception d'une fonction de hachage est un problème complexe et délicat.
Quoi qu'il en soit, et aussi performante que soit cette fonction, nous ne pouvons pas éviter les collisions. Dès lors, nous devons savoir les gérer. Il existe, pour cela, deux classes de méthodes que nous verrons plus tard, les méthodes de résolution des collisions par chaînage (méthodes indirectes) et les méthodes de résolution de collision par calcul (méthodes directes).
Fonctions de hachage
Nous allons donner maintenant quelques principes de construction de fonction de hachage. Ceux-ci sont modulables entre eux. Nous supposerons pour les exemples que les clés sont des mots représentés en mémoire par une suite de bits interprétable comme un entier.
Remarque : L'intérêt est qu'il n'y a pas besoin de calcul pour l'interprétation de la valeur.
Nous devons ensuite réduire les valeurs obtenues à l'intervalle [1,m] ou bien [0,m-1] ( il est souvent plus facile de travailler en fonction de 0 ).
Pour simplifier, nous utiliserons des caractères codés sur 5 bits et en progression croissante, soit :
A=00001$, B=00010, C=00011, ..., Z=11010
Par exemple :
BUZZ=00010101011101011010
Dès lors, le but est de construire la fonction h suivante :
définie sur une suite de bits dans un intervalle de m entiers.
Extraction
Cette méthode consiste à extraire un certains nombre de bits. Si l'on extrait p bits, l'intervalle se ramène à :
[0,2p − 1].
Pour l'exemple, effectuons l'extraction des bits 2, 7, 12 et 17 en commençant à gauche et en complétant par des zéros. Cela donne :
| NAT | 011100000110100 | 1000 | 8 |
| CARO | 00011000011001001111 | 0001 | 1 |
| REDA | 10010001010010000001 | 0000 | 0 |
| KRIS | 01011100100100110011 | 1010 | 10 |
C'est évidemment très facile à mettre en oeuvre sur ordinateur et dans le cas où m = 2p, le mot obtenu formé des p bits donne directement une valeur d'indice dans le tableau.
Le problème est que l'utilisation partielle de la clé ne donne pas de bons résultats. En effet, une bonne fonction de hachage doit utiliser tous les bits de la représentation. Celle-ci n'est bien adaptée que dans le cas où l'on connaît les données à l'avance ou bien lorsque certains bits de la codification sont non significatifs.
Compression
Dans cette méthode, nous utilisons tous les bits de la représentation que l'on découpe en sous-mots d'un nombre égal de bits que l'on combine à l'aide d'opérateur sur bits. Nous pourrions utiliser le ET ou le OU, mais ces derniers rendent systématiquement des nombres qui leur sont plus petits (ET) ou plus grand (OU). Pour cette raison, nous préférerons l'usage du OU exclusif. Pour cet exemple, nous utiliserons des sous-mots de 5 bits, Ce qui donne :
| h(NAT) | 01110 xor 00001 xor 10100 | 11011 | 27 |
| h(CARO) | 00011 xor 00001 xor 10010 xor 01111 | 11111 | 31 |
| h(REDA) | 10010 xor 00101 xor 00100 xor 00001 | 10010 | 18 |
| h(KRIS) | 01011 xor 10010 xor 01001 xor 10011 | 00011 | 3 |
Le problème de cette méthode est de "hacher" de la même manière tous les anagrammes d'une clé, par exemple :
h(REDA) = 10010 xor 00101 xor 00100 xor 00001 = 10010 = 18 h(READ) = 10010 xor 00101 xor 00001 xor 00100 = 10010 = 18
Dans ce cas de figure, c'est parce que l'on coupe les clés à la limite de définition des caractères (5 bits). Cela dit, nous pouvons toujours introduire un décalage qui permet de résoudre le problème. Il suffit de d'effectuer des rotations de bits vers la droite ; le premier caractère de 1 bit , le deuxième de 2, etc. Ce qui donne :
h(REDA) = 01001 xor 01001 xor 10000 xor 00010 = 10010 = 18 h(READ) = 01001 xor 01001 xor 00100 xor 01000 = 01100 = 12
L'exemple donné représente des clés ramenées à 5 bits, mais l'intérêt est de coder la représentation finale sur la taille d'un mot mémoire.
Division
Cette méthode consiste simplement à calculer le reste de la division par m de la valeur de la clé. Supposons que m = 23 et que nous utilisions les valeurs de compression précédentes des clés, nous obtenons alors :
| NAT = 011100000110100 | h(NAT) = 27 mod 23 = 4 |
| CARO = 00011000011001001111 | h(CARO) = 31 mod 23 = 8 |
| REDA = 10010001010010000001 | h(REDA) = 18 mod 23 = 18 |
| KRIS = 01011100100100110011 | h(KRIS) = 3 mod 23 = 3 |
Cette fonction est très facile à calculer, mais si m est pair, toutes les clés paires(impaires) iront dans des indices pairs(impairs). Il en va de même si m possède des petits diviseurs. La solution consiste à prendre un m premier. Mais là encore, il peut y avoir des phénomènes d'accumulation.
Multiplication
Soit un nombre réel θ, tel que 0 < θ < 1, on construit la fonction de hachage suivante :
C'est à dire la partie décimale du produit de x par θ, que l'on multiplie par m (taille du tableau) et dont on garde la partie entière. Ce qui pour θ = 0.5987526325, m=27 et l'utilisation des valeurs de compression précédentes des clés, donne :
| h(NAT) | 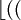 27 27 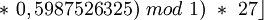
|
4 |
| h(CARO) | 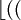 31 31 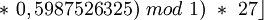
|
15 |
| h(REDA) | 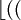 18 18 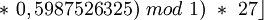
|
20 |
| h(KRIS) | 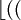 3 3 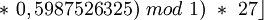
|
21 |
Avec cette méthode, la taille du tableau est sans importance, mais il faut éviter de prendre des valeurs de θ trop près de 0 ou de 1 pour éviter les accumulations aux extrémités du tableau de hachage. A priori, quelque soit la valeur que l'on choisisse, nous devrions générer des accumulations à proximité de cette valeur, mais ...
Curieusement :D, les deux valeurs de θ les plus uniformes sont statistiquement :
Conclusion : Il n'existe pas de fonction de hachage universelle. Chaque fonction doit être adaptée aux données qu'elle doit manipuler et à l'application qui les gère. Nous n'oublierons pas qu'elle doit aussi être uniforme et rapide.
Résolution des collisions
Nous supposerons pour la suite que nous disposons d'une fonction de hachage uniforme et adéquate. Plusieurs solutions possibles s'offrent alors à nous pour résoudre les collisions.
Par chaînage (méthodes indirectes)
Dans ce type de méthodes, les éléments en collision sont chaînés entre eux. Soit à l'extérieur du tableau (hachage avec chaînage séparé), soit dans une zone de débordement (hachage coalescent) si l'allocation dynamique n'est pas possible (ce qui est rarement possible ;). Je veux dire que ce ne soit pas possible).
Hachage avec chaînage séparé
Comme nous le disions, cette méthode chaîne les éléments entre eux à l'extérieur du tableau de hachage. Chaque case du tableau de hachage contient un pointeur sur une liste chaînée d'éléments dont la valeur de hachage primaire correspond à l'indice de la case du tableau.
Pour les valeurs d'exemple suivantes :
| éléments | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 |
| valeurs de hachage | 1 | 3 | 5 | 2 | 1 | 3 | 1 | 7 | 4 | 5 | 3 | 6 | 3 | 9 | 2 |
nous aurions le tableau de hachage th suivant :
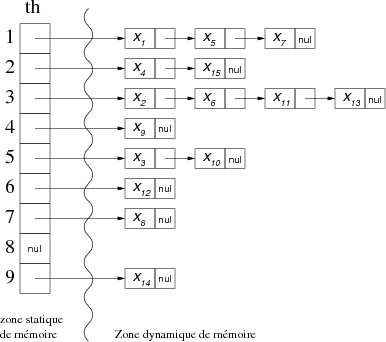
|
Remarque : Les éléments en collision pourraient être représentés sous d'autres formes (arbres, etc.), mais cela ne présente pas d'intérêt dans la mesure où : Si la fonction de répartition est uniforme et adaptée (notre postulat de départ) à la collection de données, le nombre de collision ne devrait pas excéder 5, ce qui en terme de recherche (même séquentielle :D) est tout à fait "tolérable/acceptable".
Recherche
La recherche est simple à implémenter, il suffit pour l'élément de déterminer sa valeur de hachage, et ensuite de comparer chaque élément de la liste des éléments en collision (sur cette valeur) pour déterminer si celui que l'on cherche existe ou non.
Ajout
Pour l'ajout, il y a deux possibilités :
- Recherche d'appartenance de l'élément à ajouter, et s'il n'existe pas, ajout de celui-ci en fin de liste de collision (nous y sommes déjà après la recherche). L'intérêt est de maintenir des listes courtes,
- Ajout en première place de la liste de collision. L'avantage est qu'il n'y a pas de recherche préalable, donc gain de temps. L'inconvénient est de rallonger les listes de collision.
Suppression
Comme pour l'ajout, il y a deux possibilités dont le choix dépend de celle choisie pour l'ajout :
- Recherche de l'élément à supprimer et s'il existe, suppression,
- Recherche de toutes les occurrences possibles de l'élément à supprimer et, le cas échéant, suppression. Le principal inconvénient est de devoir systématiquement parcourir toute la liste de collision.
Hachage coalescent
Si l'allocation dynamique de la mémoire n'est pas possible, il est alors nécessaire de chaîner les éléments entre eux à l'intérieur du tableau de hachage. Chaque indice de ce dernier référence alors deux champs : un élément et un lien (généralement entier) représentant l'indice du tableau où se trouve l'éventuel élément en collision primaire avec celui-ci.
Le principe est de séparer le tableau de hachage (de taille m) en deux zones :
- une zone de hachage primaire de p éléments,
- une zone de réserve de r éléments permettant de gérer les collisions.
Les contraintes sont d'avoir m=p+r supérieur ou égal au nombre d'éléments de la collection à "hacher" et un élément de lien, pour chaque valeur d'indice à l'intérieur du tableau de hachage.
Lorsqu'un élément est à placer et que sa valeur de hachage primaire atteint une case vide de la zone principale, il est placé là, sinon, il est placé dans la zone de réserve et le lien de collision est mis à jour.
Remarque : La zone de réserve est toujours utilisée en ordre décroissant d'indices.
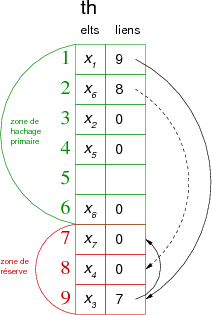
Avec p=6 et r=3, pour les valeurs d'exemple suivantes :
| éléments | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 |
| valeurs de hachage | 1 | 3 | 1 | 3 | 4 | 2 | 1 | 6 |
nous aurions le tableau de hachage th suivant :
|
Remarque : Dans ce cas, la valeur de hachage n'est plus calculée sur m, mais sur p.
Comme nous pouvons le constater, la difficulté réside dans le choix de la taille de la réserve. Sur l'exemple précédent, si nous voulions ajouter un élément dont la valeur de hachage primaire est 1, 2, 3, 4 ou 6, il serait en collision avec un autre élément déjà présent dans le tableau et nous serions dans l'impossibilité de lui trouver une place dans la mesure où la réserve est déjà pleine.
Le problème est le suivant :
- Si la réserve est trop petite, elle se remplie trop vite et l'utilisation du tableau est incomplète,
- Si la réserve est trop grande, l'effet de dispersion est perdu et une extrapolation donnerait une liste chaînée (ce qui ne présente aucun intérêt).
Dans ce cas, une solution est de ne pas considérer de zone de réserve, d'utiliser m en valeur maximale de hachage primaire et de gérer les collisions comme s'il existait une zone de réserve (en partant de l'indice maximum et en remontant).
L'inconvénient, c'est que cela crée des collisions qui ne sont pas dues à la coïncidence des valeurs de hachage primaire. On les appelle des collisions secondaires.
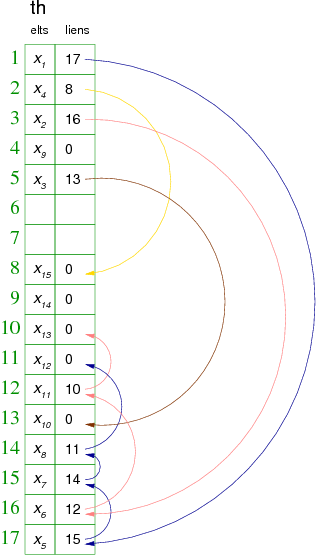
En utilisant ce principe et m=17, pour les valeurs d'exemple suivantes :
| éléments | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 |
| valeurs de hachage | 1 | 3 | 5 | 2 | 1 | 3 | 1 | 17 | 4 | 5 | 3 | 14 | 3 | 9 | 2 |
nous aurions le tableau de hachage th suivant :
|
Remarque : Nous utilisons directement les valeurs d'indice pour le lien des collisions.
Comme on peut le voir sur l'exemple précédent, au moment d'ajouter x8 de valeur de hachage primaire 17, on constate que sa place est déjà utilisée pour gérer la collision de x5 sur x1. En effet, ces deux éléments ont même valeur de hachage primaire (1). On résout le problème en posant x8 au premier emplacement libre en remontant (14) et on le lie avec sa case théorique (17). Dans ce cas, les listes de valeurs de hachage 1 et 17 fusionnent, comme d'autres par la suite. C'est ce phénomène qui est à l'origine du nom hachage coalescent.
Culture : Coalescent; Qui est soudé, réuni à un élément proche mais distinct (Petit larousse) :D
Algorithmes
Pour les algorithmes qui suivront, le type de donnée employé est le suivant :
Constantes
m = ... /* Taille du tableau de hachage */
Types
t_element = ... /* Définition du type des éléments */ t_elt = enregistrement /* Définition du type t_elt */ t_element elt entier lien fin enregistrement t_elt
t_tabhachage = m t_elt /* Définition du tableau de hachage */
Variables
t_tabhachage th
Recherche
La recherche est simple à implémenter, il suffit pour l'élément de déterminer sa valeur de hachage, et ensuite de comparer chaque élément en remontant la liste, à l'aide du lien, jusqu'à trouver l'élément recherché ou trouver un lien à zéro.
Remarque : nous ne perdons pas beaucoup de temps, puisque nous ne parcourons pas la liste fusionnée de collisions depuis le premier élément de la première liste, mais directement depuis l'indice de valeur de hachage primaire de celui que l'on cherche.
Nous allons écrire une fonction booléenne qui retourne vrai si l'élément existe et faux dans le cas contraire. Pour cela, nous allons utiliser deux fonctions externes :
* h (fonction de hachage) * estvide (fonction booléenne retournant vrai si une case est vide)
Prototypes des fonctions h et estvide :
Algorithme fonction h : entier /* compris entre 1 et m */ Paramètres locaux t_element x
Algorithme fonction estvide : booléen Paramètres locaux t_tabhachage th entier i
L'algorithme de recherche est alors :
Algorithme fonction rechercher_HachageCoalescent : booléen Paramètres locaux t_tabhachage th t_element x Variables entier i Début ih(x) /* calcul de la valeur de hachage primaire */ si estvide(th,i) alors retourne(Faux) fin si tant que th[i].elt<>x et th[i].lien<>0 faire i
th[i].lien fin tant que retourne(th[i].elt=x) Fin algorithme fonction rechercher_HachageCoalescent
Ajout
Nous allons utiliser les mêmes fonctions que pour la recherche. L'algorithme utilisera en plus une variable r (réserve) qui permettra de localiser la première case disponible (vide) en remontant. Ce qui donne :
Algorithme fonction ajouter_HachageCoalescent : booléen Paramètres globaux t_tabhachage th Paramètres locaux t_element x Variables entier r, i Début ih(x) /* calcul de la valeur de hachage primaire */ r
m /* initialisation de la place de réserve */ si estvide(th,i) alors /* ajout de l'élément */ th[i].elt
x th[i].lien
0 retourne(Vrai) fin si tant que th[i].elt<>x et th[i].lien<>0 faire i
th[i].lien fin tant que si th[i].elt=x alors /* élément déjà présent */ retourne(Vrai) fin si tant que r>=1 et non(estvide(th,r)) faire /* recherche de la 1ère place libre en réserve*/ r
r-1 fin tant que si r>=1 alors th[i].Lien
r /* mise à jour du lien avec le dernier élément de la */ th[r].Elt
x /* liste de collision sur valeur de hachage primaire */ th[r].Lien
0 retourne(Vrai) fin si retourne(Faux) /* tableau plein (no way;))*/ Fin algorithme fonction ajouter_HachageCoalescent
Remarques :
- le seul cas de retour faux est du à un tableau plein.
- Le stockage de r pourrait être envisagé pour repartir systématiquement de la dernière case utilisée pour la réserve. Dans ce cas, il faut quand même laisser la recherche de case "vide". En effet, il peut y avoir eu des ajouts directs d'éléments (sur valeur de hachage primaire) en fin de tableau.
Suppression
Hormis pour le chaînage séparé, il est relativement compliqué de gérer la suppression. En effet, sur le hachage coalescent, la suppression d'un élément nous oblige à décaler éventuellement tous ceux qui lui sont liés. Son absence peut séparer deux listes de collisions.
Pour l'exemple, imaginez que dans le tableau associé à la figure 8, nous supprimions l'élément x7 situé en place d'indice 15. Il faudrait alors décaler x8 et x12. Dans ce cas, x12 se retrouverait directement sur sa case de valeur de hachage primaire ce qui séparerait sa liste de collision ultérieure des listes de valeur de hachage 1 et 17 qui elles, seraient toujours liées.
En fait il est préférable dans ce cas de ne pas supprimer l'élément, mais de mettre en place un procédé permettant de déclarer une case non pas comme "vide", mais comme "libre". Un place pouvant alors prendre trois état : "vide", "libre" ou "occupée".
Nous pourrions alors adjoindre à la fonction estvide (précédemment déclarée) les fonctions estlibre et estoccupée, mais il est plus judicieux de n'en créer qu'une seule qui testera les trois états possibles d'une case.
Ces états sont définis à l'aide d'un type énuméré de la manière suivante :
Types
t_etat = (vide, libre, occupée) /* Définition des différents états d'une case */
Dès lors une légère modification du tableau de hachage est nécessaire pour que chaque case puisse intégrer son état, ce qui donne :
Constantes
m = ... /* Taille du tableau de hachage */
Types
t_element = ... /* Définition du type des éléments */ t_elt = enregistrement /* Définition du type t_elt */ t_etat etat /* Etat de la case */ t_element elt entier lien fin enregistrement t_elt
t_tabhachage = m t_elt /* Définition du tableau de hachage */
Variables
t_tabhachage th
Ce qui permet de faire la définition suivante de la fonction est :
Algorithme fonction est : booléen
Paramètres locaux
t_tabhachage th
entier i
t_etat etat
Début
retourne(th[i].etat=etat) /* Comparaison de l'état de la case à celui transmis en paramètre */
fin algorithme fonction est
La fonction de recherche devient alors :
Algorithme fonction rechercher_HachageCoalescent : entier Paramètres globaux t_tabhachage th Paramètres locaux t_element x Variables entier i Début ih(x) /* calcul de la valeur de hachage primaire */ tant que non(est(th,i,vide)) et non(est(th,i,occupée) et th[i].elt=x) faire si th[i].lien<>0 alors i
th[i].lien /* même si la case est libre*/ sinon sortieboucle fin si fin tant que si (est(th,i,occupée) et th[i].elt=x) alors retourne(i) sinon retourne(0) fin si Fin algorithme fonction rechercher_HachageCoalescent
Remarque : La fonction est devenue entière et retourne la place de l'élément s'il est trouvé et 0 sinon.
Grace à cela, la fonction de suppression, consistant finalement à rechercher l'élément et dans le cas où celui-ci existe à mettre la case qui le contient à "libre", utilisera directement la fonction de recherche. Il est à noter que cette fonction booléenne retournera Vrai si l'élément existait et à donc été supprimé et faux sinon, ce qui donne :
Algorithme fonction supprimer_HachageCoalescent : booléen Paramètres globaux t_tabhachage th Paramètres locaux t_element x Variables entier i Début irechercher_hachageCoalescent(th,x) /* récupération de la case contenant x s'il existe, 0 sinon*/ si i>0 alors th[i].etat
libre fin si retourne(i>0) Fin algorithme fonction supprimer_HachageCoalescent
De cette façon, les liens ne sont pas détruits et il n'y a pas besoin de reconstruire le tableau de hachage depuis le début (ou au moins depuis la création de x). Pour conclure, il nous faut donner la version de l'algorithme de la fonction ajouter incluant la gestion des cases libérées, ce qui donne :
Algorithme fonction ajouter_HachageCoalescent : booléen Paramètres globaux t_tabhachage th Paramètres locaux t_element x Variables entier r, i, lib Début ih(x) /* calcul de la valeur de hachage primaire */ si estvide(th,i) alors /* ajout de l'élément */ th[i].elt
x th[i].lien
0 th[i].etat
occupée retourne(Vrai) fin si lib
0 /* recherche de l'élément x */ tant que th[i].lien<>0 faire si est(th,i,libre) et lib=0 alors lib
i /* mémorisation de la 1ère case libre rencontrée */ fin si si est(th,i,occupée) et th[i].elt=x alors sortieboucle fin si i
th[i].lien /* même si la case est libre*/ fin tant que si lib=0 alors /* pas de case libre rencontrée */ si est(th,i,occupée) et th[i].elt=x alors /* élément déjà présent */ retourne(Vrai) fin si r
m /* initialisation de la place de réserve */ tant que r>=1 et non(estvide(th,r)) faire /* recherche de la 1ère place vide en réserve*/ r
r-1 fin tant que si r>=1 alors th[i].lien
r /* mise à jour du lien avec le dernier élément de la */ th[r].elt
x /* liste de collision sur valeur de hachage primaire */ th[r].lien
0 th[r].etat
occupée retourne(Vrai) sinon retourne(Faux) /* tableau plein (no way;))*/ fin si sinon th[lib].elt
x /* liste de collision sur valeur de hachage primaire */ th[lib].etat
occupée si est(th,i,occupée) et th[i].elt=x alors /* élément déjà présent */ th[i].etat
libre fin si retourne(Vrai) fin si Fin algorithme fonction ajouter_HachageCoalescent
Remarque : L'utilisation de la variable lib sert à mémoriser la première case libre rencontrée lors de la recherche de l'existant. Cela nous permet d'éventuellement faire avancer dans la liste de collision l'élément x s'il existait déjà. Pour mémoire, une case libre est une case qui a été occupée par un élément supprimé depuis.
Par calcul (méthodes directes)
Dans ce type de méthodes, les liens n'existent plus. L'avantage est de pouvoir utiliser leur place mémoire pour d'autres éléments. Le problème est de pouvoir gérer les collisions entre les éléments. la résolution se fait à l'aide de calcul à l'intérieur du tableau. Comme pour le hachage coalescent, m doit être supérieur ou égal au nombre d'éléments à placer.
La solution repose sur la conception d'une fonction d'essais successifs :
avec
et
.
Algorithmes
Pour les algorithmes qui suivront, le type de données employé est le suivant :
Constantes
m = ... /* Taille du tableau de hachage */
Types
t_element = ... /* Définition du type des éléments */ t_tabhachage = m t_element /* Définition du tableau de hachage */
Variables
t_tabhachage th
Recherche
Lorsque l'on recherche un élément x dans le tableau de hachage, on explore successivement les places correspondant aux essais successifs jusqu'à ce que l'on trouve x ou une case "vide". En effet, si x existait, il serait placé sur cette case "vide".
Nous allons donc écrire une fonction entière qui retourne l'indice de l'élément dans le tableau de hachage s'il existe et 0 dans le cas contraire. Pour cela, nous allons utiliser trois fonctions externes :
* h (fonction de hachage) * essai (fonction d'essais successifs) * estvide (fonction booléenne retournant vrai si une case est vide)
Prototypes des fonctions h, essai et estvide :
Algorithme fonction h : entier /* compris entre 1 et m */ Paramètres locaux t_element x
Algorithme fonction essai : entier /* compris entre 1 et m */ Paramètres locaux entier i /* N° de l'essai (compris entre 1 et m) */ t_element x
Algorithme fonction estvide : booléen Paramètres locaux t_tabhachage th entier i
L'algorithme de recherche est alors :
Algorithme fonction rechercher_Hachagedirect : entier Paramètres locaux t_tabhachage th t_element x Variables entier i, v /* i est le compteur d'essai, v la valeur de l'essai */ Début i1 tant que i<=m faire v
essai(i,x) /* calcul du ième essai */ si estvide(th,v) ou th[v]=x alors SortieBoucle fin si i
i+1 fin tant que si th[v]=x alors retourne(v) sinon retourne(0) fin si Fin algorithme fonction rechercher_Hachagedirect
Ajout
On procède comme pour la recherche. Seulement, lorsque l'on tombe sur une case "vide", on ajoute l'élément dedans. L'algorithme est sensiblement le même puisqu'il démarre par une phase de recherche, nous conserverons donc les mêmes fonctions externes.
Nous allons donc écrire une fonction entière qui retourne le numéro d'indice si l'élément existe après la tentative d'ajout (qu'il est pu être créé ou qu'il existait déjà) et 0 dans le cas contraire (tableau plein). L'algorithme d'ajout est alors :
Algorithme fonction ajouter_Hachagedirect : entier Paramètres globaux t_tabhachage th Paramètres locaux t_element x Variables entier i, v /* i est le compteur d'essai, v la valeur de l'essai */ Début i1 tant que i<=m faire v
essai(i,x) /* calcul du ième essai */ si estvide(th,v) ou th[v]=x alors SortieBoucle fin si i
i+1 fin tant que si th[v]=x alors retourne(v) sinon si estvide(th,v) alors th[v]
x retourne(v) sinon retourne(0) fin si fin si Fin algorithme fonction ajouter_Hachagedirect
Remarques :
- Il pourrait être judicieux de vérifier que le tableau n'est pas plein avant de commencer la recherche. Cela dit, avec
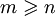 , il est peu probable que cela arrive.
, il est peu probable que cela arrive.
- Utiliser rechercher_hachagedirect dans ajouter_Hachagedirect est envisageable, mais peu intéressant compte tenu de la simplicité de l'algorithme de recherche. Rappelons qu'un appel de fonction prendra plus de temps que le code "inline".
Suppression
Nous avons déjà constaté que la suppression générait un problème de réorganisation des données. Nous allons retenir la solution retenue pour le hachage coalescent. Nous allons donc reprendre la définition des états des cases ainsi que celle de la fonction est qui utilisera les déclarations suivantes :
Constantes
m = ... /* Taille du tableau de hachage */
Types
t_element = ... /* Définition du type des éléments */ t_elt = enregistrement /* Définition du type t_elt */ t_etat etat /* Etat de la case */ t_element elt fin enregistrement t_elt
t_tabhachage = m t_elt /* Définition du tableau de hachage */
Variables
t_tabhachage th
La fonction de recherche devient alors :
Algorithme fonction rechercher_Hachagedirect : entier Paramètres locaux t_tabhachage th t_element x Variables entier i, v /* i est le compteur d'essai, v la valeur de l'essai */ Début i1 tant que i<=m faire v
essai(i,x) /* calcul du ième essai */ si est(th,v,vide) ou (est(th,v,occupée) et th[v].elt=x) alors SortieBoucle fin si i
i+1 fin tant que si est(th,v,occupée) et th[v].elt=x alors retourne(v) sinon retourne(0) fin si Fin algorithme fonction rechercher_Hachagedirect
La procédure de suppression se contente, quant à elle, de rechercher x et de marquer sa case comme "libre", soit :
Algorithme procedure supprimer_Hachagedirect Paramètres globaux t_tabhachage th Paramètres locaux t_element x Variables entier v /* v est la valeur de l'essai concluant ou 0 sinon*/ Début vrechercher_Hachagedirect(th,x) si v>0 alors th[v].etat
libre fin si Fin algorithme procedure Supprimer_Hachagedirect
Là encore, il ne nous reste plus, pour conclure, qu'à donner la version de l'algorithme de la fonction ajouter incluant la gestion des cases "libres", ce qui donne :
Algorithme fonction ajouter_Hachagedirect : entier Paramètres globaux t_tabhachage th Paramètres locaux t_element x Variables entier i, v, lib /* i est le compteur d'essai, v la valeur de l'essai, lib la 1ère case libre */ Début i1 lib
0 tant que i<=m faire v
essai(i,x) /* calcul du ième essai */ si est(th,v,vide) alors SortieBoucle fin si si est(th,v,occupée) et th[v].elt=x alors retourne(v) fin si si est(th,v,libre) et lib=0 alors lib
v fin si i
i+1 fin tant que si est(th,v,vide) alors si lib=0 alors th[v].elt
x th[v].etat
occupée retourne(v) sinon th[lib].elt
x th[lib].etat
occupée retourne(lib) fin si sinon retourne(0) fin si Fin algorithme fonction ajouter_Hachagedirect
Remarque : Comme pour le hachage coalescent, cet algorithme pourrait être modifié de telle sorte que dès que l'on trouve une case "libre" ou "vide" on ajoute x. Si à l'arrivée, on détecte x et que l'ajout à été fait, on supprime ce dernier. L'intérêt est de rapprocher x de ses premiers essais de valeur de hachage et donc de réduire le temps des prochaines recherche.
Les différentes méthodes de hachage direct se caractérisent par le choix de la fonction des essais successifs. cette dernière associe une suite de m places dans le tableau. Il y a au plus m! suites différentes dans le tableau, mais la plupart des méthodes en utilisent beaucoup moins. Dans le hachage linéaire, par exemple, on voit que la suite des places disponibles d'un élément dépend uniquement de sa valeur de hachage primaire (1er essai). Ce qui implique qu'il y a uniquement m suites différentes dans le tableau de hachage.
Hachage linéaire
Le hachage linéaire fonctionne de la façon suivante : Lorsqu'il y a collision sur une case d'indice v, on essaie la case d'indice v+1. Si l'on est sur la mième case (la dernière), on repasse à la 1ière.
Appelons Modulo plus cette progression circulaire et notons la 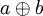
A l'aide d'une fonction de hachage uniforme h, la suite d'essais successifs serait :
essai1(x) = h(x)
...
...
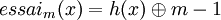
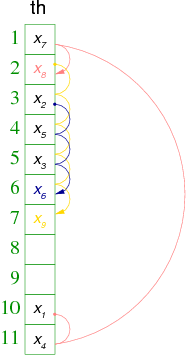
En utilisant ce principe et m=11, pour les valeurs d'exemple suivantes :
| éléments | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 |
| valeurs de hachage | 10 | 3 | 5 | 11 | 4 | 3 | 1 | 10 | 2 |
nous aurions le tableau de hachage th suivant :
|
Remarques :
- Les éléments qui ont la même valeur de hachage primaire ont la même séquence d'essais.
- Plus les groupements sont importants (en taille), plus la probabilité de voir leur taille augmenter est importante.
Un avantage de cette méthode est de ne pas avoir à écrire la fonction d'essais successifs. En fait, il suffit de remplacer dans les algorithmes l'appel initial à cette fonction par un appel à la fonction de hachage et de remplacer les appels suivants par 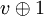 .
.
Ce qui donnerait pour l'algorithme de recherche :
Algorithme fonction rechercher_Hachagelinéaire : entier Paramètres globaux t_tabhachage th Paramètres locaux t_element x Variables entier i, v, lib /* i est le compteur d'essai, v la valeur de l'essai, lib la 1ère case libre */ Début i1 lib
0 v
h(x) /* calcul du 1er essai */ tant que i<=m faire si est(th,v,vide) ou (est(th,v,occupée) et th[v].elt=x) alors SortieBoucle fin si si est(th,v,libre) et lib=0 alors lib
v fin si i
i+1 v
v mod m + 1 /* calcul du ième essai */ fin tant que si lib=0 alors si i>m alors /* pas trouvé et tableau plein => problème */ retourne(0) sinon si est(th,v,vide) alors /* pas trouvé */ retourne(0) sinon /* trouvé en v au ième essai */ retourne(v) fin si fin si sinon si i>m ou est(th,v,vide) alors /* pas trouvé */ retourne(0) sinon th[lib].elt
x th[lib].etat
occupée th[v].etat
libre retourne(lib) fin si fin si Fin algorithme fonction rechercher_Hachagelinéaire
Remarques :
- L'algorithme tient compte de la possibilité de supprimer les éléments et donc des trois états possibles des cases du tableau de hachage. Ce qui permet deux choses dans le cas de la recherche :
- différencier les cas pas trouvé du cas pas trouvé et tableau plein
- déplacer l'élément trouvé vers une case libre rencontrée lors de ses essais précédents
- C'est une version "brute de décoffrage" bien évidemment simplifiable :)
Double hachage
Un des problèmes soulevés par le hachage linéaire est la formation de groupements d'éléments. La probabilité qu'un groupement de k éléments sur un tableau de taille m voit sa taille augmenter au prochain ajout est de 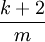 .
.
Il faut donc essayer de disperser un peu plus les éléments en cas de collision. Nous pouvons alors imaginer la fonction d'essais suivante :
où k est un entier fixé.
Pour que la séquence de m essais référence les m valeurs, il faut que k et m soient premiers entre eux. En fait, cela ne règlera pas vraiment le problème d'accumulation d'éléments, mais ceux-ci se produiront de k en k. Pour éviter cela, il faudrait que l'incrément (k) dépende de l'élément x.
On introduit alors une deuxième fonction de hachage d (double hachage) et la séquence d'essais devient :
Là encore, il faut que chaque séquence d'essais nous garantisse les m valeurs. Ce qui répond au même critère que précédemment, à savoir que m et d(x) doivent être premiers entre eux quel que soit x.
Cela peut s'obtenir des deux façons suivantes :
* m est premier et
* m = 2p (il est pair) et d(x) doit être impair pour tous les x.
Ce que l'on peut obtenir en ayant d(x) = 2d'(x) + 1, où d'(x) est une fonction dont les valeurs appartiennent à [0,2p − 1 − 1].
Remarque : Nous n'allons pas développer à nouveau les algorithmes de recherche et d'ajout dans la mesure où l'adaptation est "simplissime" (remplacement des initialisations et de 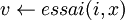 par
par 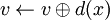 ).
).
Conclusion sur les méthodes de hachage
- Toutes ces méthodes sont bien adaptées aux ensemble statique. Elles sont à peu près équivalentes pour un faible taux de remplissage.
- Le hachage coalescent est la méthode la plus efficace si la zone de mémoire réservée au hachage doit être fixée à l'avance (zone de data statique).
- Le hachage linéaire est le moins rapide, mais cette méthode présente l'avantage d'être extrêmement simple à mettre en oeuvre.
- Le double hachage est plus performant que le hachage linéaire, mais il nécessite le calcul de deux fonctions de hachage (et donc leur écriture).
- A part le chaînage séparé, elles supportent assez mal les suppressions y compris avec un système de marquage qui augmenterait considérablement les temps de recherche.
- La plus performante d'entre elles est incontestablement le chaînage séparé.
(Christophe "krisboul" Boullay)
![h\ :\ \{0,1\}^{*} \rightarrow [0,m-1]](https://algo.infoprepa.epita.fr/images/math/4/5/e/45ea13772350895d40a49aafe0881723.png)
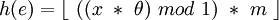
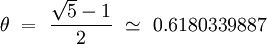
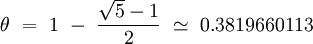
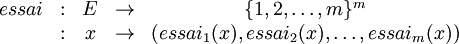
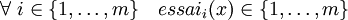
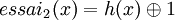
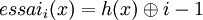
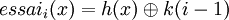
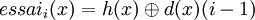
![d \in [1, m-1]](https://algo.infoprepa.epita.fr/images/math/a/e/b/aeb7c27a81a0b4baa5928f9bd348a04b.png)