Epita:Algo:Cours:Info-Sup:Structures séquentielles
Sommaire |
Les listes linéaires
La liste linéaire est la forme la plus simple d'organisation de données que l'on puisse rencontrer. Celles-ci sont stockées les unes à la suite des autres dans des places et permettent divers traitements séquentiels. L'ordre des éléments dans une liste ne dépend pas des éléments eux-mêmes, mais de la place de ceux-ci dans la liste. Il y a plusieurs façons de décrire une liste, soit itérativement, soit récursivement. Nous allons envisager les deux et voir sur quels types de fonctionnement elles sont respectivement basées et quelle représentation mémoire est la mieux adaptée suivant le type de liste. En effet, il nous faut pouvoir créer des éléments, en modifier et en supprimer. De plus (et pour le même prix), nous y ajouterons des fonctionnalités propres aux listes comme la concaténation, la recherche d'élément etc.
Le type liste récursive
types
liste, place
utilise
élément
opérations
listevide :liste cons : liste x élément
liste fin : liste
liste tête : liste
place contenu : place
élément premier : liste
élément succ : place
place
préconditions
fin(l) est-défini-ssi l ≠ listevide tête(l) est-défini-ssi l ≠ listevide premier(l) est-défini-ssi l ≠ listevide
axiomes
premier(l) = contenu(tête(l)) fin(cons(e,l)) = l premier(cons(e,l)) = e succ(tête(l)) = tête(fin(l))
avec
liste l élément e
Nous ne redonnerons plus par la suite la terminologie des éléments utilisés dans les définitions de type (Oui, c'est vrai, ça ira bien comme ça !).
Alors dans le type abstrait qui précède, nous avons :
- Liste et Place comme types définis
- élément comme type prédéfini
- tête et succ comme opérations internes de place
- contenu comme observateur de place
- listevide, fin et cons comme opérations internes de liste
- premier comme observateur de liste
Ces opérations n'étant pas définies partout, il y bien sur des préconditions. La définition algébrique affecte aux diverses fonctions les rôles suivants :
- liste-Vide crée une liste sans éléments (une sorte de "constructeur")
- tête permet de récupérer la première place (celle de tête)
- contenu permet d'obtenir l'élément d'une place
- premier permet d'obtenir le premier élément d'une liste (sans place intermédiaire)
- fin permet de détruire l'élément de tête et de récupérer la liste restante
- cons permet d'ajouter un élément en première place (en l'insérant devant la liste existante)
- succ permet de passer à la place suivante
Le type Liste itérative
types
liste, place
utilise
entier, élément
opérations
listevide :liste accès : liste x entier
place contenu : place
élément ième : liste x entier
élément longueur : liste
entier supprimer : liste x entier
liste insérer : liste x entier x élément
liste succ : place
place
préconditions
accès(l,k) est-défini-ssi l ≠ listevide & 1 ≤ k ≤ longueur(l) supprimer(l,k) est-défini-ssi l ≠ listevide & 1 ≤ k ≤ longueur(l) insérer(l,k,e) est-défini-ssi 1 ≤ k ≤ longueur(l)+1
axiomes
longueur(listevide) = 0 longueur(supprimer(l,k)) = longueur(l)-1 longueur(insérer(l,k,e)) = longueur(l)+1
1 ≤ i < kième(supprimer(l,k),i) = ième(l,i) k ≤ i ≤ longueur(l)-1
ième(supprimer(l,k),i) = ième(l,i+1)
1 ≤ i < kième(insérer(l,k,e),i) = ième(l,i) k = i
ième(insérer(l,k,e),i) = e k < i ≤ longueur(l)+1
ième(insérer(l,k,e),i) = ième(l,i-1)
contenu(accès(l,k)) = ième(l,k) succ(accès(l,k)) = accès(l,k+1)
avec liste l entier i,k élément e
Cette présentation correspond à une autre forme d'implémentation des listes linéaires. En fait l'opération de base n'est plus l'accès à la première place d'une liste, mais l'opération accès qui renvoie la Kième place de cette liste. Les autres opérations découlant de ce fonctionnement.
Le type abstrait liste itérative bien que plus adapté à d'autres fonctionnements, permet aussi de décrire des traitements récursifs.
Ce qui est important, c'est de comprendre qu'en fait nous décrivons la même donnée, seule la manière de s'en servir diffère. Une façon simple de le montrer est de décrire les opération d'un type en terme de celles de l'autre et inversement.
Prenons par exemple, les opérations du type récursif en terme des opérations du type itératif:
| récursive | ⇔ | itérative |
| tête (l) | accès (l,1) | |
| premier (l) | ième (l,1) | |
| fin (l) | supprimer (l,1) | |
| cons (e,l) | insérer (l,1,e) |
Et inversement:
| itérative | ⇔ | récursive |
| insérer (l,i,e) | l2 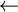 liste-vide liste-vide
| |
| (i-1) fois | 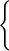
|
l2 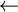 cons (premier (l),l2) cons (premier (l),l2)
|
l 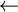 fin (l) fin (l)
| ||
l 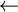 cons (e,l) cons (e,l)
| ||
| (i-1) fois | 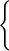
|
l 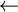 cons (premier (l2),l) cons (premier (l2),l)
|
l2 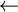 fin (l2) fin (l2)
|
Comme on peut le constater, dans ce cas la correspondance ne se résume pas une simple opération, mais l'opération insérer à bien été retranscrite en terme des opérations de la liste récursive.
Remarque : La traduction des autres opérations est laissée en exercices.
Extensions du type liste
Bien entendu, nous avons souvent besoin d'opérations complémentaires sur les listes comme la concaténation de deux listes, la recherche d'un élément dans une liste. Dans ce cas, et ceci est valable pour n'importe quel type défini, on déclare ce que l'on appelle des extensions au type. Il est alors inutile de représenter le type abstrait qui est supposé connu (En tous cas, on l'espère!). Pour ces deux opérations supplémentaires, nous présenterons le profil (Le bon, hein Tintin !) les éventuelles préconditions et les axiomes pour une liste itérative et pour une liste récursive.
Concaténation
La concaténation de deux listes est l'opération qui permet de les rassembler en les mettant bout à bout. Les éléments de chacune conservent leur place d'origine au sein de leur propre liste, la deuxième liste étant accrochée à la suite de la première.
opérations
concaténer : liste x listeliste
axiomes (Liste récursive)
concaténer(listevide,l) = l concaténer(cons(e,l),l2) = cons(e,concaténer(l,l2))
axiomes (Liste itérative)
longueur(concaténer(l,l2)) = longueur(l)+longueur(l2) 1 < i < longueur(l)ième(concaténer(l,l2),i) = ième(l,i) longueur(l)+1 < i < longueur(l)+longueur(l2)
ième(concaténer(l,l2),i) = ième(l2,i-longueur(l))
avec
liste l,l2 entier i élément e
Recherche d'un élément
La recherche consiste à trouver un élément dans une liste et à retourner sa place si celui-ci existe dans la liste. Dans ce cas (j'aime bien cette locution. Et de plus, je fais ce que je veux ! C'est clair Junior !?), le problème est que la recherche n'est pas définie pour un élément non présent. Il faut donc une précondition sur la recherche que l'on décrira à l'aide d'une opération auxiliaire existe.
opérations
rechercher : élément x listeplace existe : élément x liste
booléen
préconditions
rechercher(e,l) est-défini-ssi existe(e,l) = vrai
axiomes (Liste récursive)
existe(e,listevide) = faux e = e2existe(e2,cons(e,l)) = vrai e ≠ e2
existe(e2,cons(e,l)) = existe(e2,l) existe(e,l) = vrai
contenu(rechercher(e,l)) = e
axiomes (Liste itérative)
existe(e,listevide) = faux e = e2existe(e2,insérer(l,i,e)) = vrai e ≠ e2
existe(e2,insérer(l,i,e)) = existe(e2,l) existe(e,l) = vrai
contenu(rechercher(e,l)) = e
avec
liste l entier i élément e,e2
Représentation des Listes
Les listes comme tous les autres types de données sont implémentables de différentes manières. Les deux formes basiques sont la représentation statique (à l'aide de tableaux) et la représentation dynamique (à l'aide de pointeurs et d'enregistrements).
Bien sûr, pour des types de données plus élaborés, il sera possible de représenter ceux-ci par des hybrides des deux (statique et dynamique). De plus, il sera éventuellement possible d'avoir plusieurs représentations statiques et plusieurs dynamiques (C'est chouette ! Non ?).
Représentation statique
Exemple de déclaration algorithmique :
Constantes
Nbmax = 20
Types
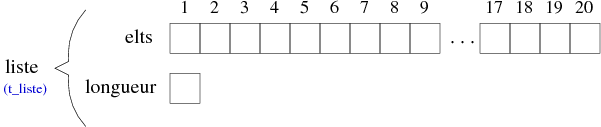
t_element = ... /* Définition du type des éléments */ t_vectNbmaxelts = Nbmax t_element /* Définition du tableau des éléments */ t_liste = enregistrement /* Définition du type t_liste */ t_vectNbmaxelts elts entier longueur fin enregistrement t_liste
Variable
t_liste liste
Ce qui correspondrait à la structure suivante :
|
Le problème posé par les tableaux est la nécessité d'un surdimensionnement. En effet, ils sont statiques. Donc pour être sûr que votre liste de données puisse y être représentée, vous êtes tenus de donner au tableau une taille supérieure à celle de la liste (pour d'éventuels ajouts). Dès lors, vous devez savoir où s'arrêtent vos données dans ce tableau. C'est l'utilité de la variable longueur qui contiendra toujours la taille de votre liste. Pour accèder à une donnée il suffit alors de préciser le nom du tableau et le rang de celle-ci. C'est très simple (un enfant de 5 ans comprendrait. Enfin, je crois...).
Remarque 1 : Pour insérer ou supprimer une donnée, vous devrez décaler dans un sens où dans l'autre tous les éléments se trouvant entre celle-ci et la fin de votre liste, ce qui ne rend pas cette représentation très performante en cas de modifications fréquentes des éléments.
Remarque 2 : Contrairement à ce que l'on pourrait croire, cette représentation est parfaitement adaptée aux listes récursives, où la longueur fait office de place de tête et où il n'a aucun transfert de valeur a effectuer au milieu du tableau.
Représentation dynamique
Exemple de déclaration algorithmique :
Types
t_element = ... /* Définition du type des éléments */ t_pliste =t_liste /* Définition du type pointeur t_pliste */ t_liste = enregistrement /* Définition du type t_liste */ t_element elt t_pliste lien fin enregistrement t_liste
Variables
t_pliste liste
Ce qui correspondrait à la structure suivante :

|
Le pointeur NUL représente la fin de liste (listevide). Cette représentation utilise à priori plus de place que la précédente dans la mesure où l'on doit stocker la valeur des pointeurs. Mais en fait, le nombre d'éléments est toujours celui de la liste, ni plus ni moins. Contrairement à l'implémentation statique pour laquelle il faut surdimensionner le tableau, celle-ci ne nécessite pas de compteur du nombre d'éléments (Longueur).
Remarque : L'inconvénient majeur est de ne pas pouvoir accèder au Kième élément directement. Par contre, il est facile de concaténer deux chaînes, d'ajouter ou de supprimer un élément sans avoir à tout décaler. Elle est de plus très bien adaptée aux traitements récursifs.
Variantes de représentation
Utilisation d'une sentinelle en tête
Une possibilité est de ne pas utiliser un pointeur sur l'enregistrement, mais directement un enregistrement pour générer la tête de liste. L'avantage est de ne pas avoir besoin de traitement particulier en insertion devant le premier élément. Dans ce cas, l'élément de l'enregistrement de tête n'est pas utilisé et la déclaration de variables est :
Variable
t_liste liste
Ce qui correspondrait à la structure suivante :

|
Liste circulaire
On peut aussi utiliser des listes circulaires. Dans ce cas, le dernier pointeur n'est pas nul, mais il pointe sur le premier élément de la liste. Pour cela, le pointeur principal de liste référence le dernier élément et non pas le premier. Dans ce cas, pour obtenir l'élément de tête, il suffit d'avancer d'un lien.
Notons que si la liste n'est composée que d'un élément, celui-ci pointe sur lui-même (Ah Ouais! C'est Géniaaallll !). La déclaration est alors la même que pour la représentation dynamique de base.
Ce qui correspondrait à la structure suivante :

|
Note : On pourrait là aussi utiliser une sentinelle (un enregistrement) à la place d'un pointeur
Liste doublement chaînée
Le problème des représentations précédentes est de ne pouvoir aller que dans un sens. En effet, les listes étant généralement ordonnées, il peut être intéressant de revenir sur l'élément précédent, or cette possibilité n'existe pas. Pour y arriver, il suffit de rajouter un lien en sens inverse. Dans ce cas, il faut posséder non seulement un pointeur de tête, mais aussi un pointeur de queue. La déclaration devient :
Types
t_element = ... /* Définition du type des éléments */ t_penreg =t_enreg /* Définition du type pointeur t_penreg */ t_enreg = enregistrement /* Définition du type t_enreg */ t_element elt t_penreg suivant,precedent fin enregistrement t_enreg t_liste = enregistrement /* Définition du type t_liste */ t_penreg premier,dernier fin enregistrement t_liste
Variable
t_liste liste
Ce qui correspondrait à la structure suivante :

|
Bien sûr, il est toujours possible de construire d'autres structures comme par exemple; une liste circulaire doublement chaînée. Enfin pour terminer sur les variantes possibles des listes, citons la simulation de pointeurs dans un tableau. Dans ce cas, les éléments du tableau sont des enregistrements contenant deux champs; l'élément et un entier contenant l'indice de l'élément suivant. Tout est possible ou presque, mais utiliser ce genre de structure n'a aucun intérêt dans la mesure où elle présente tous les inconvénients du statique et du dynamique réunis (un peu comme le Side-Car).
Les piles et les files
Les piles
Les piles sont des structures LIFO (Last In First Out). C'est à dire que les entrées et les sorties s'effectuent du même coté. L'image la plus simple que l'on puisse donner est la pile d'assiette où, si l'on est totalement "terminé" (ce qui pour certains étudiants n'est pas gagné), les entrées et les sorties se font au même endroit. On appelle ce dernier le sommet de la pile.
Le type abstrait d'une pile est le suivant :
types
pile
utilise
booléen, élément
opérations
pilevide :pile empiler : pile x élément
pile dépiler : pile
pile sommet : pile
élément estvide : pile
booléen
préconditions
dépiler(p) est-défini-ssi estvide(p) = Faux sommet(p) est-défini-ssi estvide(p) = Faux
axiomes
dépiler(empiler(p,e)) = p sommet(empiler(p,e)) = e estvide(pilevide) = Vrai estvide(empiler(p,e)) = Faux
avec
pile p élément e
Représentation statique des piles
Nous avons besoin d'un tableau pour ranger les éléments et d'un entier Sommet qui nous permette de savoir en permanence où se situe celui-ci. Pour avoir quelque chose de systémique, nous allons déclarer une pile statique comme la composée d'un ensemble de valeurs empilées (un vecteur d'éléments) et d'un indicateur de sommet (entier), ce qui donne:
Exemple de déclaration algorithmique :
Constantes
Nbmax = 20 /* Nombre maximum d'éléments dans la pile */
Types
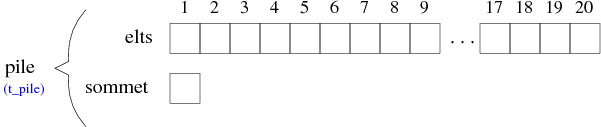
t_element = ... /* Définition du type des éléments */ t_elements = Nbmax t_element /* Définition du vecteur d'éléments */ t_pile = enregistrement /* Définition du type pile */ t_elements elts entier sommet fin enregistrement t_pile
Variable
t_pile pile
Ce qui correspondrait à la structure suivante :
|
Représentation dynamique des piles
Dans ce cas, les éléments de la pile sont chaînés entre eux, et le pointeur représente le sommet de celle-ci. On peut noter que le lien sur les éléments est un lien de précédence qui permet lorsque l'on dépile de savoir quel élément avait été précédemment empilé.
Exemple de déclaration algorithmique :
Types
t_element = ... /* Définition du type des éléments */ t_ppile =t_pile /* Définition du type pointeur t_ppile */ t_pile = enregistrement /* Définition du type t_pile */ t_element elt t_ppile precedent fin enregistrement t_pile
Variables
t_ppile pile
Ce qui correspondrait à la structure suivante :

|
Les files
Les files sont des structures FIFO (First In First Out). C'est à dire que les entrées et les sorties s'effectuent à chaque extrémité de la liste. L'image la plus simple que l'on puisse donner est la file d'attente où (en l'absence de tout resquilleur) la première personne arrivée dans la file sera la première à en sortir. Nous avons donc besoin dans ce cas là de maitriser la position de l'entrée et celle de la sortie. On référence alors la Tête et la Queue de la file.
Le type abstrait d'une pile est le suivant :
types
file
utilise
booléen, élément
opérations
filevide :file enfiler : file x élément
file défiler : file
file premier : file
élément estvide : file
booléen
préconditions
défiler(f) est-défini-ssi estvide(f) = Faux premier(f) est-défini-ssi estvide(f) = Faux
axiomes
estvide(f) = Vraipremier(enfiler(f,e)) = e estvide(f) = Faux
premier(enfiler(f,e)) = premier(f) estvide(f) = Vrai
défiler(enfiler(f,e)) = filevide estvide(f) = Faux
défiler(enfiler(f,e)) = enfiler(défiler(f),e) estvide(filevide) = Vrai estvide(enfiler(f,e)) = Faux
avec
file f élément e
Représentation statique des files
Nous avons besoin d'un tableau pour ranger les éléments et de deux entiers Tete et Queue qui nous permettent de savoir en permanence où se situe le début et la fin de la file.
Exemple de déclaration algorithmique :
Constantes
Nbmax = 8 /* Nombre maximum d'éléments dans la file */
Types
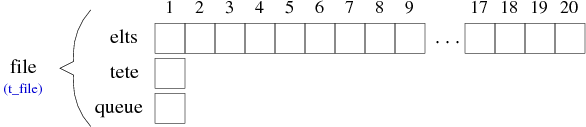
t_element = ... /* Définition du type des éléments */ t_elements = Nbmax t_element /* Définition du vecteur d'éléments */ t_file = enregistrement /* Définition du type file */ t_elements elts entier tete,queue fin enregistrement t_file
Variable
t_file file
Ce qui correspondrait à la structure suivante :
|
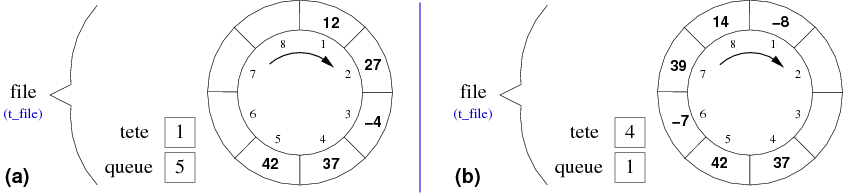
Nous pourrions pour visualiser l'implémentation d'une file statique utiliser cette figure, mais en fait pour illustrer les débordements, il vaut mieux représenter celle-ci de façon circulaire, ce qui donnerait pour deux cas différents:
|
Pour ces deux exemples, nous avons fixé Nbmax à 8. En fait les valeurs de tete et de queue avancent d'un rang à chaque fois, exception faite de la bascule de 8 à 1. En effet, lorsque nous atteignons la limite Nbmax que ce soit avec la tete ou la queue, nous passons à 1 alors que dans les autres cas, nous passons à la valeur augmentée de 1. Ce dépassement est géré de façon extrêmement simple, il suffit d'utiliser un modulo Nbmax, soit 8 dans le cas présent.
Représentation dynamique des files
Dans ce cas, les éléments de la file sont chaînés entre eux, et les pointeurs Tête et Queue représentent les deux extrémités de celle-ci.
Exemple de déclaration algorithmique :
Types
t_element = ... /* Définition du type des éléments */ t_penr =t_enr /* Définition du type pointeur t_penr */ t_enr = enregistrement /* Définition du type t_file */ t_element elt t_penr suivant fin enregistrement t_enr
t_file = enregistrement /* Définition du type file */ t_penr tete,queue fin enregistrement t_file
Variables
t_file file
Ce qui correspondrait à la structure suivante (a) :
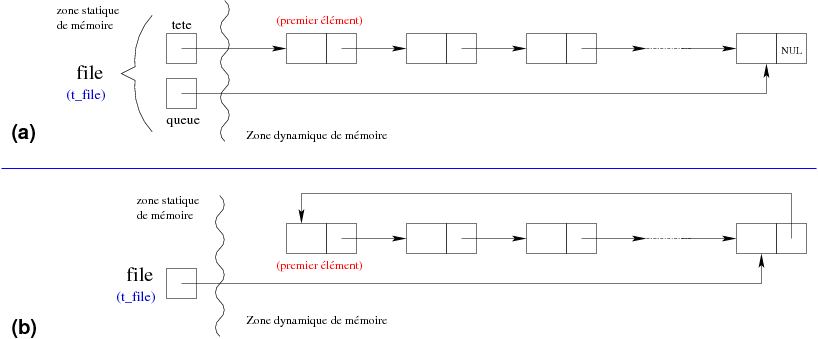
|
On peut remarquer que dans le cas d'une représentation circulaire (b), le pointeur de Tête n'a plus aucune utilité. Il suffit de suivre le lien Suivant à partir du dernier pour déterminer le premier élément. Il est, d'autre part, possible d'utiliser le système de sentinelle utilisée avec les listes, à savoir prendre un élément complet pour les deux pointeurs (Tête et Queue).
(Christophe "krisboul" Boullay)