Epita:Algo:Cours:Info-Sup:Algorithmes de recherche de base

Définitions

On appelle recherche associative le fait que le critère de recherche ne porte que sur la valeur de la clé de l’élément recherché.

On appelle recherche positive le fait que la clé recherchée soit présente dans la collection de données.

On appelle recherche négative le fait que la clé recherchée soit absente de la collection de données.

Recherche séquentielle

Cette recherche est extrêmement simple et convient parfaitement aux collections de données de petite taille. A moins que ce soient toujours les mêmes éléments que l’on recherche et que l’on ait dans ce cas adapté la liste.

Dans une liste non triée

L’algorithme est le plus simple qui soit. Il consiste à parcourir chaque élément de la liste séquentiellement et à le comparer avec la clé. Si l’on possède une liste l de n éléments, que l’on cherche l’élément x, et que l’on considère une fonction booléenne retournant vrai si la recherche est positive et faux si elle est négative, on obtient l’algorithme suivant :

algorithme fonction rechercher : booléen
Paramètres locaux
   liste    l
   élément  x
Variables
   entier   i
Début
   i $\leftarrow$ 1
   tant que i <= longueur(l) faire   /* Nombre d’éléments de la liste */
      si x=ième(l,i) alors
      retourne(Vrai)                  /* Recherche positive */
      fin si
      i $\leftarrow$ i + 1
   fin tant que
   retourne(Faux)                     /* recherche négative */
fin algorithme fonction rechercher

Dans ce cas de figure, la complexité est au pire d’ordre n (cf les listes) et en moyenne déterminée par la probabilité que l’élément x se trouve à la i ^ème place. Malheureusement nous ne connaissons pas, en général, les probabilités de positionnement des différents éléments. Donc nous allons faire en sorte que ceux que l’on recherche le plus fréquemment se retrouvent en tête de liste.

Recherche auto-adaptative

Cette recherche est une adaptation de la précédente, elle ne peut être appliquée que sur des listes non triées puisque qu’elle modifie l’ordre des éléments au gré de la recherche. Il existe plusieurs variantes possibles :

• l'agressive : Chaque fois que l’on trouve un élément, on le place directement en tête de liste. Cette méthode n’est facilement applicable qu’aux listes représentées de manière chaînée dans la mesure où sur une représentation contiguë, il faudrait décaler les éléments se trouvant entre la tête et celui que l’on vient de chercher. Le problème est d'amener aux premières places des éléments très peu recherchés.

• la molle : Chaque fois que l’on trouve un élément, on le fait progresser d’une place vers la tête de liste. Cette méthode est facilement applicable aux deux formes de représentation (contiguë ou chaînée) puisque ce n'est en fait qu'une permutation de valeurs. Le problème est de ne faire progresser les élements recherchés que très doucement : Il faudrait 2000 recherches successives d'un élément se trouvant à la 2001 ^ème place pour le faire parvenir en tête de liste.

• la plus raisonnable : Chaque fois que l’on trouve un élément, on le fait progresser d’un certain nombre de places vers la tête de liste (par exemple de la moitié de la distance entre lui et le premier élément). Cette méthode est facilement applicable à la représentation contiguë et présente deux avantages : celui de faire progresser, assez vite, les éléments vers la tête et celui de ne pas positionner d’artefact en tête de liste (élément recherché une seule fois). C'est la représentation chaînée qui est, dans ce cas, la plus intéressante. En effet, il suffit de posséder un pointeur qui progresse moins vite que celui de recherche (deux fois moins dans le cas de la moitié de la distance) pour savoir à chaque instant ou se trouve la nouvelle position de l'élément recherché.

Dans une liste triée

L’algorithme et sa complexité sont les mêmes que pour la liste non triée avec toutefois un avantage pour la recherche négative. En effet, les éléments étant ordonnés, il est facile de savoir si l’on a dépassé une valeur permettant de trouver l’élément. Imaginons une liste numérique triée de manière croissante. Nous recherchons 12 et la liste est constituée des éléments {1,2,3,6,9,11,13,15,21,38,42}. Lorsque nous arrivons sur l’élément 13, nous sommes sûrs de ne plus pouvoir trouver le 12. Cela dit, la complexité au pire reste la même (recherche d’un élément plus grand que le dernier).

L’algorithme très légèrement modifié donne :

algorithme fonction rechercher : booléen
Paramètres locaux
   liste    l
   élément  x
Variables
   entier   i
Début
   i $\leftarrow$ 1
   tant que (i <= longueur(l)) et (x <> ième(l,i)) faire   /* Nombre d’éléments de la liste */
      si x=ième(l,i) alors
      retourne(Vrai)                  /* Recherche positive */
      fin si
      i $\leftarrow$ i + 1
   fin tant que
   retourne(Faux)                     /* recherche négative */
fin algorithme fonction rechercher

Recherche dichotomique

Cette méthode impose que la liste des éléments soit triée. De plus elle n’est applicable que sur des représentations contiguës de liste (statique). Soit une liste l, et un élément x recherché et m le milieu de la liste l, alors le principe de la recherche dichotomique est le suivant :

• x = ième(l,m) alors on a trouvé x et la recherche s’arrête

• x > ième(l,m) alors x se trouve après m s'il existe. On poursuit donc la recherche sur la moitié supérieure de la liste l

• x < ième(l,m) alors x se trouve avant m s'il existe, on poursuit donc la recherche sur la moitié inférieure de la liste l

La recherche se poursuit ainsi en coupant en deux le nombre d’éléments restant à traiter après chaque comparaison. Si la recherche se termine sur une liste vide, cela veut dire que l’élément x n’existe pas et que la recherche est négative.

L’algorithme de la recherche dichotomique (version récursive), retournant l’entier correspondant à la place de l’élément dans la liste s’il existe, et 0 s’il n’existe pas, est :

algorithme fonction recherche_dichotomique : booléen
Paramètres locaux
   liste    l
   élément  x
   entier   g,d                    /* Bornes gauche et droite de la liste l */
Variables
   entier   m                      /* indice du médian de la liste l */
Début
   si g<=d alors
      m $\leftarrow$ (g+d) div 2
      si x=ième(l,m) alors
         retourne(m)               /* Recherche positive */
      sinon
         si x<ième(l,m) alors
            retourne(recherche_dichotomique(l,x,g,m-1))
         sinon
            retourne(recherche_dichotomique(l,x,m+1,d))
         fin si
      fin si
   sinon
      retourne(0)                  /* Recherche négative */
   fin si 
fin algorithme fonction recherche_dichotomique

Remarque: Pour rechercher sur l’intégralité de la liste, il suffit de passer, respectivement, les valeurs 1 et longueur(l) à g et d.

Le même algorithme version itérative:

algorithme fonction recherche_dichotomique_iterative : booléen
Paramètres locaux
   liste    l
   élément  x
   entier   g,d                    /* Bornes gauche et droite de la liste l */
Variables
   entier   m                      /* indice du médian de la liste l */
Début
   tant que g<=d faire
      m $\leftarrow$ (g+d) div 2
      si x=ième(l,m) alors
         retourne(m)               /* Recherche positive */
      sinon
         si x<ième(l,m) alors
            d $\leftarrow$ m-1
         sinon
            g $\leftarrow$ m+1
         fin si
      fin si
   fin tant que
   retourne(0)                     /* Recherche négative */
fin algorithme fonction recherche_dichotomique_iterative

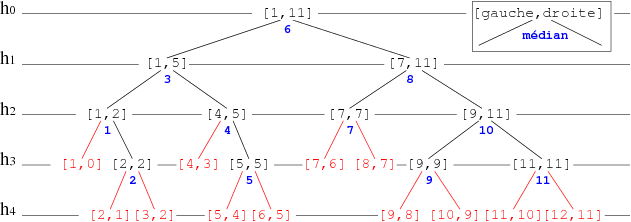
Une représentation de l'exécution de cet algorithme appliquée à une liste triée de 11 éléments peut être donnée à l'aide de l'arbre de décision représenté figure 1. Chaque Noeud représente l'intervalle de recherche : Les bornes gauche et droite ainsi que l'indice calculé du médian (en bleu). Si l'élément se trouve à cette place la recherche se termine positivement, sinon on continue sur l'axe approprié (à gauche ou à droite selon que la valeur recherchée est plus petite ou plus grande que celle de l'élément médian. Si les bornes se croisent (lien et intervalle représentés en rouge) la recherche se termine négativement.

Remarque: les indices médian calculés représentent toutes les positions possibles de la liste. Ainsi si l'élément existe, il ne pourra pas nous échapper (Gnark! Gnark! Gnark!).

Figure 1. Arbre de décision de la recherche dichotomique sur une liste de 11 éléments.

Cette représentation nous permet d'analyser facilement le nombre de comparaisons effectuées par la recherche dichotomique. En fait l'algorithme parcourt une branche jusqu'à tomber (au pire) sur un intervalle non défini. Dans le cas de la recherche psoitive, le nombre de comparaisons est égal à 2*hauteur(v)+1 avec v le noeud dont l'indice médian correspond à celui de l'élément recherché. L'arbre étant équilibré, cette hauteur est majorée par log₂ n avec n la puissance de 2 supérieure ou égale au nombre d'éléments de la liste. sur notre exemple de 11 éléments log₂ 16 = 4.

Recherche de la première occurrence d’un élément

Dans le cas où la liste présente plusieurs occurrences des éléments, il peut être intéressant d’en vouloir une précise. Supposons que cela soit la première occurrence que l’on recherche, il faut absolument conserver le principe dichotomique et ne pas partir en recherche séquentielle lorsque l’on se trouve sur une occurrence quelconque de l’élément recherché. En effet, tout le bénéfice de la dichotomie pourrait se trouver réduit à néant du fait de l’éloignement de la première occurrence par rapport à celle sur laquelle nous nous trouvons. Par conséquent, nous allons reprendre la version itérative de la recherche dichotomique et lui appliquer les modifications nécessaires, soit itérativement :

algorithme fonction recherche_dichotomique_premocc_iterative : booléen
Paramètres locaux
   liste    l
   élément  x
   entier   g,d                    /* Bornes gauche et droite de la liste l */
Variables
   entier   m                      /* indice du médian de la liste l */
Début
   tant que g<d faire
      m $\leftarrow$ (g+d) div 2
      si x<ième(l,m) alors
         d $\leftarrow$ m-1
      sinon
         g $\leftarrow$ m+1
      fin si
   fin tant que
   si x=ième(l,g) alors            /* g ou d */
      retourne(m)                  /* Recherche positive */
   sinon
      retourne(0)                  /* Recherche négative */
   fin si
fin algorithme fonction recherche_dichotomique_premocc_iterative

Recherche par interpolation linéaire

La recherche par interpolation nécessite aussi une liste triée en représentation contiguë. Son principe est similaire à celui de la dichotomie. La différence réside dans le calcul de la place de l’élément. Dichotomiquement, on utilise un élément central (le médian), l’interpolation elle, estime la place par rapport à l’agencement des données.

Par exemple, lorsque dans un dictionnaire vous cherchez le mot « Cacahuètes », vous n’ouvrez pas le dictionnaire au milieu, mais plutôt au début, là où vous pensez avoir le plus de chance de trouver le mot "Cacahuètes". C’est le principe de la recherche par interpolation : estimer la place probable de l’élément recherché.

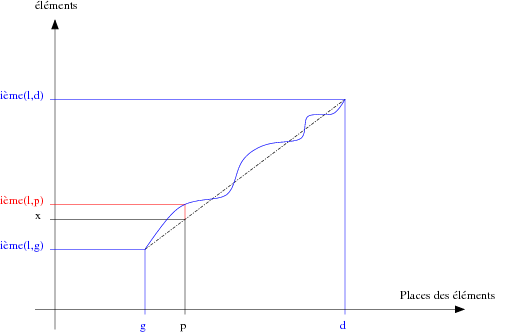
Prenons une collection de données l triées en ordre croissant; Supposons que la progression de ces données est linéaire. Lorsque l’on cherche l’élément x entre des bornes gauche g et droite d, il semble intéressant d’aller voir à la place p définie par p = g + ((d - g) * (x - ième(l,g) div (ième(l,d) - ième(l,g)), comme sur l’exemple Figure 2.

Figure 2. Exemple de recherche par interpolation linéaire.

Cette fonction n'est que le rapport des distances entre d'une part les éléments gauche, droit et x de la liste l et d'autre part les bornes gauche, droite et la place supposée de l'élément x de cette même liste l (Théorème de Thalès).

Comme le montre l'exemple de la figure 2, nous avons la vraie fonction de répartition des éléments de la liste l représentée en bleu. Supposons la position de l'élément recherché x, on interpole alors sa place en p en se basant sur une progression linéaire (ligne noire pointillée). La question est de savoir si le p^ième élément de l est bien x. Sur cet exemple, il est clair que non.

Comme la dichotomie, cette méthode utilise le fait qu’une liste soit triée. De plus elle n’est applicable que sur des représentations contiguës de liste.Soit une liste l, x un élément recherché et p la place estimée de l’élément recherché dans la liste l, alors le principe de la recherche par interpolation est le suivant :

• x = ième(l,p) alors on a trouvé x et la recherche s’arrête

• x > ième(l,p) alors x se trouve probablement après p, on poursuit donc la recherche sur la partie supérieure restante de la liste l

• x < ième(l,p) alors x se trouve probablement avant p, on poursuit donc la recherche sur la partie inférieure restante de la liste l

La recherche se poursuit ainsi en interpolant le nombre d’éléments restant à traiter après chaque comparaison. Si la recherche se termine sur une liste vide, cela veut dire que l’élément x n’existe pas et que la recherche est négative.

L’algorithme de la recherche par interpolation (version récursive), retournant l’entier correspondant à la place de l’élément dans la liste s’il existe, et 0 s’il n’existe pas, est :

algorithme fonction recherche_interpolation : booléen
Paramètres locaux
   liste    l
   élément  x
   entier   g,d                    /* Bornes gauche et droite de la liste l */
Variables
   entier   p                      /* indice de la place estimée de l'élément recherché */
Début
   si g<=d alors
      p $\leftarrow$ g + ((d - g) * (x - ième(l,g) div (ième(l,d) - ième(l,g))
      si x=ième(l,p) alors
         retourne(p)               /* Recherche positive */
      sinon
         si x<ième(l,p) alors
            retourne(recherche_interpolation(l,x,g,p-1))
         sinon
            retourne(recherche_interpolation(l,x,p+1,d))
         fin si
      fin si
   sinon
      retourne(0)                  /* Recherche négative */
   fin si 
fin algorithme fonction recherche_interpolation

Le même algorithme version itérative:

algorithme fonction recherche_interpolation_iterative : booléen
Paramètres locaux
   liste    l
   élément  x
   entier   g,d                    /* Bornes gauche et droite de la liste l */
Variables
   entier   p                      /* indice de la place estimée de l'élément recherché */
Début
   tant que g<=d faire
      p $\leftarrow$ g + ((d - g) * (x - ième(l,g) div (ième(l,d) - ième(l,g))
      si x=ième(l,p) alors
         retourne(p)               /* Recherche positive */
      sinon
         si x<ième(l,p) alors
            d $\leftarrow$ p-1
         sinon
            g $\leftarrow$ p+1
         fin si
      fin si
   fin tant que
   retourne(0)                     /* Recherche négative */
fin algorithme fonction recherche_interpolation_iterative

Remarques:

• La difficulté par rapport à la dichotomie est de donner une bonne fonction d’interpolation, l’idéal étant d’avoir une fonction de répartition uniforme des éléments dans la liste. En terme de complexité, si n est le nombre d’éléments de la liste, la dichotomie est de l’ordre log₂ n et l’interpolation (si la répartition est uniforme) de l’ordre de log₂ (log₂ n)

• Cela semble beaucoup plus intéressant que la dichotomie, mais il y a un bémol: il faut que les données de la liste soient numériques ou numérisables rapidement. En effet, la clé intervient dans le calcul de la place, ce qui n'est pas le cas pour la dichotomie. D'où une perte de temps de calcul pas forcément négligeable. D'autre part, il faut que la liste soit très grande pour que la différence entre log₂ n et log₂ (log₂ n) soit suffisamment grande.

---

(Christophe "krisboul" Boullay)