Epita:Algo:Cours:Info-Sup:Arbres de recherche

Dans les méthodes de base, nous avons vu que l'on pouvait obtenir des temps de recherche logarithmique sur des structures séquentielles en représentation contiguë. L'idéal serait de pouvoir obtenir les mêmes performances sur des structures dynamiques. Cela n'est pas possible avec des structures séquentielles, en revanche cela l'est avec les structures arborescentes, donc...

les arbres binaires de recherche (ABR)

N'importe quelle collection de n éléments dont les clés appartiennent à un ensemble ordonné peut être stockée et classée à l'intérieur d'un arbre binaire de n noeuds. Dans ce cas, les noeuds contiennent les éléments et les liens père-fils permettent de gérer l'ordre entre ces éléments.

Un ABR est un arbre binaire étiqueté tel qu'en tout noeud v de l'arbre:

- les éléments du sous-arbre gauche de l'arbre de racine v sont inférieurs ou égaux à celui contenu dans v,

- les éléments du sous-arbre droit de l'arbre de racine v sont strictement supérieurs à celui contenu dans v.

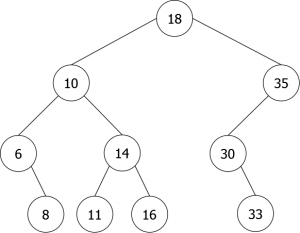
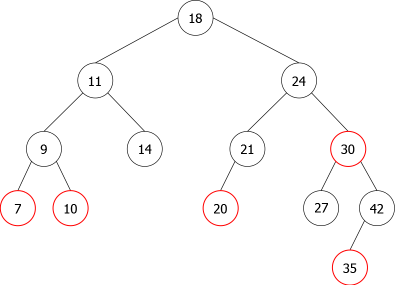
Il peut y avoir plusieurs ABRs représentant un même ensemble de données, comme le montre l'exemple suivant (cf. figure 1), pour l'ensemble d'entiers E = {6,8,10,11,14,16,18,30,33}.

Figure 1. Exemple de deux arbres binaires de recherche possibles d'un même ensemble d'entiers.

Recherche dans un ABR

L'opération de recherche d'un élément x dans un ABR B définie abstraitement par :

opérations

   rechercheABR : element x abr $\rightarrow$ booléen

répond au principe suivant :

- si B est un arbre vide, la recherche est négative
- si x est égal à l'élément de la racine de B, la recherche est positive
- si x est inférieur à l'élément de la racine de B, la recherche se poursuit sur le sous-arbre gauche de B
- si x est supérieur à l'élément de la racine de B, la recherche se poursuit sur le sous-arbre droit de B

L’algorithme correspondant à ce principe serait le suivant :

algorithme fonction rechercherABR : booléen
Paramètres locaux
   élément  x
   abr      B
Début
   si B = arbrevide alors   
      retourne(Faux)                        /* recherche négative : échec */
   sinon   
      si x=contenu(racine(B) alors
         retourne(Vrai)                     /* Recherche positive : succès */
      sinon
         si x<contenu(racine(B) alors
            retourne(chercherABR(x,g(B)))   /* poursuite dans sous-arbre gauche */
         sinon
            retourne(chercherABR(x,d(B)))   /* poursuite dans sous-arbre droit */
         fin si
      fin si
   fin si
fin algorithme fonction rechercherABR

Ajout dans un ABR

L'opération d'ajout d'un élément x dans un ABR B peut se faire de deux manières, en feuille ou en racine de l'arbre B.

Ajout en feuille

L'opération d'ajout d'un élément x en feuille d'un ABR B définie abstraitement par :

opérations

   ajouterfeuilleABR : element x abr $\rightarrow$ abr

répond au principe suivant :

- déterminer la place d'adjonction
- réaliser l'adjonction

La première partie se fait sur le même principe que la recherche, le dernier appel récursif se terminant sur un arbre vide. Il ne reste plus ensuite qu'à créer un nouveau noeud (une nouvelle feuille) contenant l'élément x à ajouter. Ce qui pourrait donner l'algorithme suivant :

algorithme fonction ajouterfeuilleABR : arbrebinaire
Paramètres locaux
   élément  x
   abr      B
Variables
   noeud  r
Début
   si B = arbrevide alors   
      contenu(r) $\leftarrow$ x
      retourne(<r,arbrevide,arbrevide>)  /* retour de l'arbre réduit au noeud créé */
   sinon   
      si x <= contenu(racine(B) alors
         retourne(<racine(B),ajouterfeuilleABR(x,g(B)),d(B)>)   /* retour de l'arbre avec ajout dans sous-arbre gauche */
      sinon
         retourne(<racine(B),g(B),ajouterfeuilleABR(x,d(B))>)   /* retour de l'arbre avec ajout dans sous-arbre droit */
      fin si
   fin si
fin algorithme fonction ajouterfeuilleABR

Construction d'un ABR par ajouts successifs en feuille

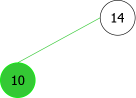
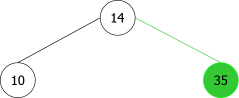
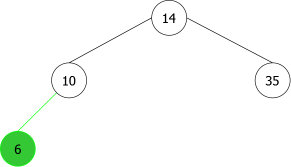
En appliquant l'algorithme précédent pour les entiers suivants : 14, 10, 35, 6, 30, 33, 11, 16, 8, 18 nous aurions la séquence de construction suivante d'ABRs:

Figure 2. Construction d'un ABR par ajouts successifs des valeurs 14, 10, 35, 6, 30, 33, 11, 16, 8 et 18.

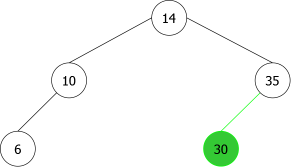
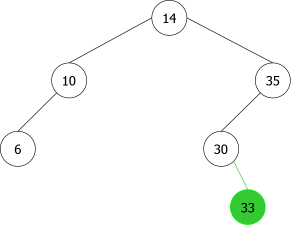
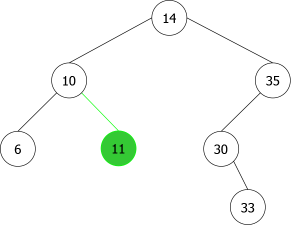
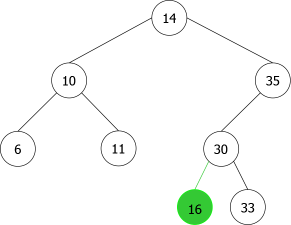
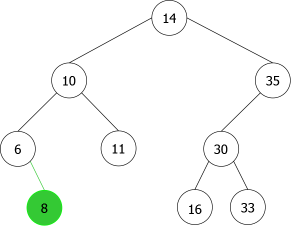
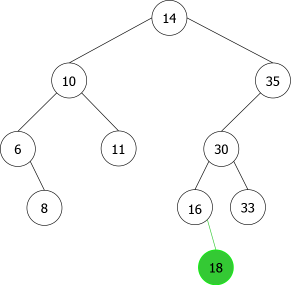
Ajout en racine

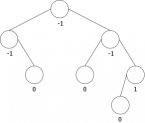
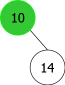
Le problème est que l'on ne peut pas se contenter simplement d'ajouter le nouveau noeud racine contenant l'élément x en se basant sur l'élément de l'actuelle racine. Ce qui positionnerait cette dernière comme fils gauche ou droit de la nouvelle racine. En effet, cela ne permettrait pas de respecter à coup sûr la relation d'ordre, comme le montre la séquence d'ajouts en racine des éléments {35, 10, 14} (cf. Figure 3).

Figure 3. Mauvaise construction d'un ABR par ajouts successifs des valeurs 35, 10, 14 en racine.

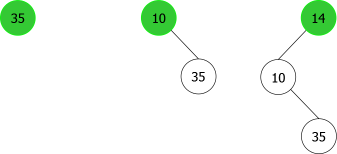
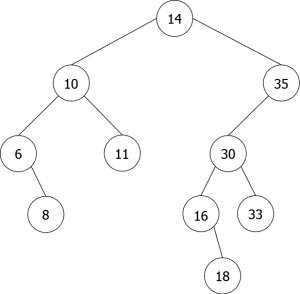
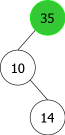
On voit bien sur cet exemple qu'au troisième ajout en racine (celui de 14), le 35 se retrouve dans le sous-arbre gauche ce qui n'est pas possible. En effet, 35 est bien supérieur à 10, mais aussi à 14, il devrait donc se situer dans le sous-arbre droit de l'arbre de racine 14, ce que montre la figure 4.

Figure 4. Construction correcte d'un ABR par ajouts successifs des valeurs 35, 10, 14 en racine.

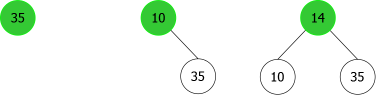
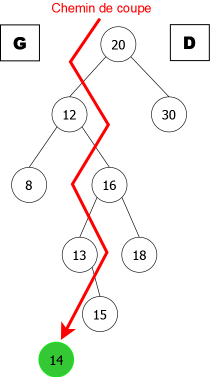
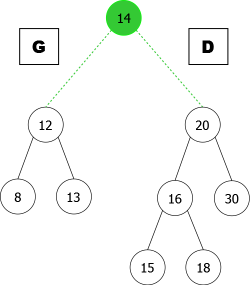
Pour régler ce problème, il faudrait répartir dans les sous-arbres gauche (appelé G) et droit (appelé D) du nouvel arbre créé par l'ajout en racine de l'élément x, les éléments existants de B selon qu'ils sont inférieurs ou supérieurs à x.

On va alors suivre le chemin (appelé chemin de coupe) allant de la racine de l'arbre B jusqu'à la nouvelle feuille accueillant x si l'ajout se faisait en feuille. A chaque noeud rencontré, on va regarder si l'élément de celui-ci est inférieur(resp. supérieur) à x. S'il est inférieur (resp. supérieur), il ira dans G(resp. D) accompagné implicitement de son propre sous-arbre gauche(resp. droit) cont enant des éléments qui lui sont plus petits(resp. grands) donc implicitement inférieurs(resp. supérieurs) à x.

Il ne reste plus ensuite qu'à accrocher G et D à la nouvelle racine x, comme le montre l'exemple de la figure 5.

Figure 5. Exemple d'ajout en racine de 14 sur un ABR..

L'opération d'ajout d'un élément x en racine d'un ABR B définie abstraitement par :

opérations

   ajouterracineABR : element x abr $\rightarrow$ abr

va nous permettre d'ajouter l'élément x dans une nouvelle racine de l'arbre B et non pas dans une nouvelle feuille. L'utilité de cet ajout est de pouvoir, tout en respectant la relation d'ordre, insérer un nouvel élément n'importe où dans un ABR (pas seulement à la racine). Elle répond au principe suivant :

- Créer le nouveau noeud contenant x
- couper B en deux arbres G et D selon le chemin de coupe
- accrocher G et D au noeud contenant x

Nous allons donc avoir besoin d'une procédure réalisant la coupe de l'ABR B en deux sous-arbres G et D selon la valeur de x. Ce qui donne l'algorithme suivant :

algorithme procedure couper
Paramètres locaux
   élément  x
Paramètres globaux
   abr      B, G, D
Début
   si B = arbrevide alors   /* fin de récursion et fermeture des liens G et D */
      G $\leftarrow$ arbrevide           
      D $\leftarrow$ arbrevide
   sinon
      si x < contenu(racine(B)) alors
         D $\leftarrow$ B
         couper(x, g(B), G, g(D))  /* récursion sur le sous-arbre gauche et mise en attente du fils gauche de D */
      sinon   
         G $\leftarrow$ B
         couper(x, d(B), d(G), D)  /* récursion sur le sous-arbre droit et mise en attente du fils droit de G */       
      fin si
   fin si
fin algorithme procedure couper

Il est à noter que cette version de l'algorithme d'ajout en racine (procédure couper comprise), ne construit pas les arbres G et D pour les accrocher ensuite, mais elle les construit au fur et à mesure qu'elle parcourt le chemin de coupe. Dans ce cas, l'appel de la procédure couper se fait directement sur les fils gauche et droit du noeud créé comme nouvelle racine. La procédure d'appel ajouterracineABR pourrait alors être la suivante:

algorithme procedure ajouterracineABR
Paramètres locaux
   élément  x
Paramètres globaux
   abr      B
Variables
   abr      R
Début
   contenu(racine(R)) $\leftarrow$ x
   couper(x, B, g(R), d(R))   /* appel de couper avec les fils de R pour G et D */
   B $\leftarrow$ R
fin algorithme procedure ajouterracineABR

Construction d'un ABR par ajouts successifs en racine

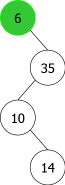
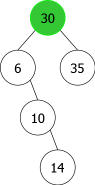
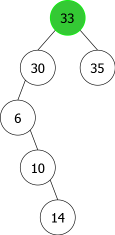
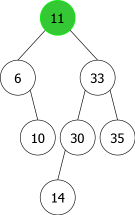
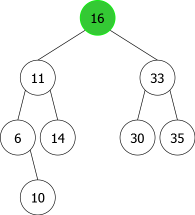
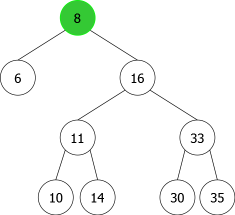
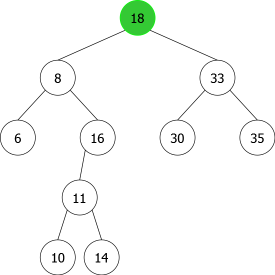
En appliquant l'algorithme précédent pour les entiers suivants : 14, 10, 35, 6, 30, 33, 11, 16, 8, 18 nous aurions la séquence de construction suivante d'ABRs:

Figure 6. Construction d'un ABR par ajouts successifs des valeurs 14, 10, 35, 6, 30, 33, 11, 16, 8 et 18.

Suppression dans un ABR

L'opération de suppression d'un élément x dans un ABR B définie abstraitement par :

opérations

   supprimerABR : element x abr $\rightarrow$ abr

répond au principe suivant :

- déterminer la place de l'élément à supprimer
- réaliser la suppression
- réorganiser éventuellement l'arbre

La première partie se fait sur le même principe que la recherche. Il ne reste plus ensuite qu'à déterminer à quel type de noeud (contenant l'élément x à supprimer) nous avons affaire. En effet, celui-ci peut être de trois types différents avec les implication suivantes :

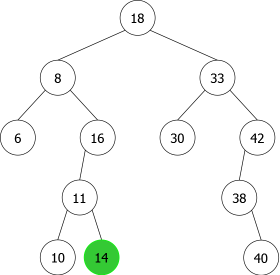
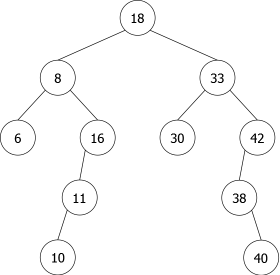
1. Le noeud contenant x est une feuille comme pour la suppression de 14 sur figure 7(a). Dans ce cas, le noeud est simplement détruit et l'arbre obtenu est celui de la figure 7(b).
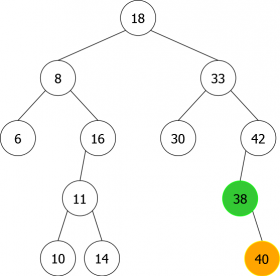
2. Le noeud contenant x est un point simple, comme pour la suppression de 38 (point simple à droite) sur figure 8(a). Dans ce cas, le noeud est simplement détruit et remplacé par son fils (droit dans le cas présent). L'arbre obtenu est celui de la figure 8(b) ou le noeud 40 est venu remplacer le 38.
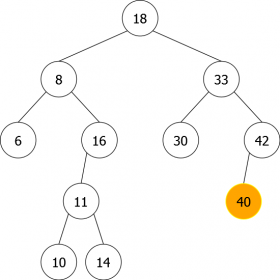
3. Le noeud contenant x est un point double, comme pour la suppression de 18 (racine de l'arbre) sur figure 9(a). Dans ce cas, deux possibilités s'offrent à nous pour ne pas avoir à reconstruire complètement l'arbre:
   • Remplacer l'élément du noeud par son immédiat inférieur (bout du bord droit du sous-arbre gauche), le noeud 16 sur cet exemple.
   • Remplacer l'élément du noeud par son immédiat supérieur (bout du bord gauche du sous-arbre droit), le noeud 30 sur cet exemple.

L'intérêt de cette méthode est double

• une fois le remplacement fait, il n'y a plus qu'à détruire le noeud remplaçant (16 ou 30 sur cet exemple) qui ne peut-être qu'une feuille ou un point simple
• la relation d'ordre est conservée aisément dans la mesure où le plus grand des plus petits est toujours inférieur au plus petit des plus grands et réciproquement.
  

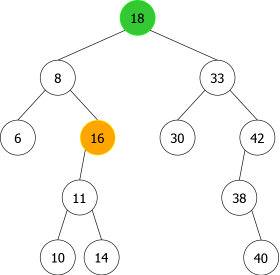
Sur l'exemple de la figure 9, nous avons choisi de le remplacer par son immédiat inférieur (le plus grand des plus petits). L'arbre obtenu est celui de la figure 9(b) ou le noeud 16 est venu remplacer le 18 et a été détruit et remplacé simplement par son fils gauche 11 comme dans le cas 2 (point simple).

Figure 7. Suppression du noeud 14 (feuille).

(a)	(b)

Figure 8. Suppression du noeud 38 (point simple à droite).

(a)	(b)

Figure 9. Suppression du noeud 18 (point double).

(a)	(b)

Remarque: Ces deux solutions sont équivalentes s'il n'y a pas de redondance de valeurs dans l'ABR.

Nous allons avoir besoin de deux opérations supplémentaires pour pouvoir répondre au problème de la suppression d'un point double. Les deux opérations sont définies abstraitement par :

opérations

    max : abr $\rightarrow$ element
   dmax : abr $\rightarrow$ abr

Elles répondent aux principes suivants :

- max(B) retourne le plus grand élément de l'ABR B
- dmax(B) retourne l'ABR B amputé de son plus grand élément

Nous allons les réunir en une seule opération suppmax, ce qui pourrait donner l'algorithme suivant :

algorithme procédure suppmax
Paramètres globaux
   élément  max
   abr      B
Début
   si d(B) = arbrevide alors      /* pas de fils droit, nous sommes sur le plus grand élément de l'arbre */
      max $\leftarrow$ contenu(racine(B))
      B $\leftarrow$ g(B)
   sinon   
      suppmax(max, d(B))          /* poursuite à droite */
   fin si
fin algorithme procédure suppmax

Il ne reste plus alors qu'à écrire l'algorithme de la procédure de suppression d'un élément x dans un ABR B, ce qui pourrait donner l'algorithme suivant :

algorithme procédure supprimerABR 
Paramètres locaux
   élément  x
Paramètres globaux
   abr      B
Variables
   élément max
Début
   si B <> arbrevide alors   
      si x < contenu(racine(B)) alors   
         supprimerABR(x, g(B))
      sinon
         si x > contenu(racine(B)) alors   
            supprimerABR(x, d(B))
         sinon       /* x = contenu(racine(B)), x est trouvé => destruction. */
            si g(B) = arbrevide alors /* B est un point simple à droite ou une feuille */
               B $\leftarrow$ d(B)
            sinon  
               si d(B) = arbrevide alors /* B est un point simple à gauche */
                  B $\leftarrow$ g(B)
               sinon  /* B est un point double => appel à suppmax */
                  suppmax(max, g(B))
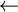                  contenu(racine(B)) $\leftarrow$ max
               fin si
            fin si
         fin si
      fin si
   fin si
fin algorithme procédure supprimerABR

Pour cet algorithme, on a décidé arbitrairement de faire la recherche et ensuite de gérer la suppression lorsque l'élément est trouvé. Nous aurions tout aussi bien pu faire l'inverse. Cela ne change en rien la complexité de cet algorithme et dans le deuxième cas, il se rapprocherait plus du schéma de l'algorithme de recherche qui effectivement traite le "trouvé" avant le "essaie encore".

Analyse du nombre de comparaisons (complexité des précédents algorithmes)

Les algorithmes de recherche, d'adjontion et de suppression procèdent par comparaisons de valeurs (x = contenu(racine(B)), x < contenu(racine(B)), x > contenu(racine(B))). La comparaison entre deux éléments est l'opération fondamentale, celle qui va nous permettre de faire l'analyse de ces algorithmes et de déterminer leurs performances. Or le nombre de comparaisons effectuées entre deux valeurs par ces algorithmes peut être lu directement sur l'ABR manipulé, en effet :

• pour la recherche:
  • si elle se termine positivement sur un noeud v, le nombre de comparaisons effectuées est 2*profondeur(v)+1
  • si elle se termine négativement après le noeud v, le nombre de comparaisons effectuées est 2*profondeur(v)+2

• pour l'ajout:
  • en feuille: la recherche de position se termine toujours négativement après un noeud v. Mais le nombre de comparaisons est divisé par deux puisque l'on se demande si x<=contenu(racine(B)). Le nombre de comparaisons effectuées est alors profondeur(v)+1
  • en racine: le nombre de comparaisons est le même puisque l'algorithme compare l'élément à insérer à ceux du chemin de recherche de l'ajout en feuille (chemin de coupe). Le nombre de comparaisons effectuées est donc là aussi profondeur(v)+1

• pour la suppression: Le nombre de comparaisons est identique à celui de l'algorithme de recherche. Cela étant, si l'on tient compte du temps de recherche de l'élément de remplacement (cas de la suppression d'un point double), il faut ajouter la complexité de la procédure suppmax.

Conclusion: L'analyse, basée sur le nombre de comparaisons, des algorithmes de recherche, d'adjonction et de suppression d'un élément dans un arbre binaire de recherche se ramène à l'étude de la profondeur des noeuds dans l'ABR. La profondeur moyenne d'un ABR de n éléments est comprise entre n si l'arbre est dégénéré et 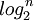$log_2^n$ s'il est complet ou parfait (cf. Arbres binaires particuliers).

Le problème est que les algorithmes d'ajout et de suppression ne garantissent pas l'équilibre de l'ABR et que dans ce cas il ne nous reste plus qu'à miser sur la chance ou à modifier nos algorithmes pour que ceux-ci nous assurent l'équilibrage des arbres de recherche. C'est cette deuxième solution que nous allons retenir et dont traite le chapitre suivant.

Les arbres de recherche équilibrés

Dans le chapitre précédent, nous avons vu que la complexité des opérations de recherche, d'ajout et de suppression pouvait être au pire linéaire. Cela est du au fait qu'un arbre binaire n’est pas nécessairement équilibré, et que dans le pire des cas, il peut être filiforme. Imaginez un ajout aux feuilles avec comme entrées successives la liste {a,b,c,d,e,f}.

Pour conserver, cette complexité logarithmique, nous devons donc équilibrer l’arbre. Dans ce cas, il est clair que la réorganisation de celui-ci doit être la plus rapide possible. Ce qui impliquera un léger déséquilibre de l’arbre. Nous allons étudier deux classes d’arbres équilibrés, les A-V.L. (arbre binaires) et les Arbres 2.3.4 (arbres généraux). Pour chacune de ces classes, les complexités des algorithmes de recherche, d’ajout et de suppression seront logarithmiques.

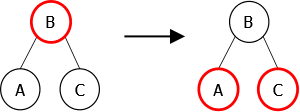
Rotations

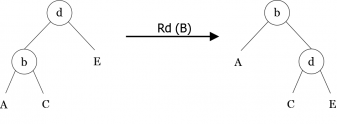
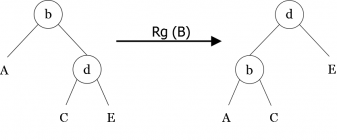
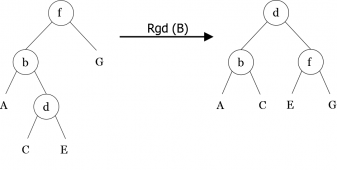
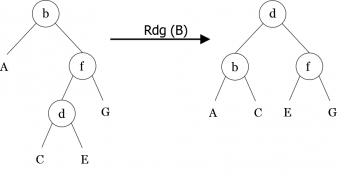
Dans un premier temps, nous allons implémenter des algorithmes de rééquilibrage appelés rotations. Ils effectuent des transformations locales de l’arbre et sont au nombre de quatre : rotation simples (gauche et droite) ; rotation double (gauche-droite et droite-gauche). Des exemples de ces rotations sont montrés en figures 10, 11, 12 et 13.

Figure 10. Rotation droite de l'arbre B.

Figure 11. Rotation gauche de l'arbre B.

Figure 12. Rotation gauche-droite de l'arbre B.

Figure 13. Rotation droite-gauche de l'arbre B.

Spécification formelle

Ces quatre opérations (Rg, Rd, Rgd et Rdg) sont définies de la manière suivante :

opérations

   rg  : arbrebinaire $\rightarrow$ arbrebinaire
   rd  : arbrebinaire $\rightarrow$ arbrebinaire
   rgd : arbrebinaire $\rightarrow$ arbrebinaire
   rdg : arbrebinaire $\rightarrow$ arbrebinaire

préconditions

   rg(C) est-défini-ssi C ≠ arbrevide & d(C) ≠ arbrevide
   rd(C) est-défini-ssi C ≠ arbrevide & g(C) ≠ arbrevide
   rgd(C) est-défini-ssi C ≠ arbrevide & g(C) ≠ arbrevide & d(g(C)) ≠ arbrevide
   rdg(C) est-défini-ssi C ≠ arbrevide & d(C) ≠ arbrevide & g(d(C)) ≠ arbrevide

axiomes

  rg(< b, A, < d, C, E > >) = < d, < b, A, C >, E >
  rd(< d, < b, A, C >, E >)= < b, A, < d, C, E > >
  rgd(< f, < b, A, < d, C, E > >, G >)= < d, < b, A, C >, < f, E, G > >
  rdg(< b, A, < f, < d, C, E >, G > >)= < d, < b, A, C >, < f, E, G > >

avec

  arbrebinaire A, C, E, G
  noeud        b, d, f

Algorithme (Procédure rg)

algorithme procédure Rg
Paramètres globaux
   arbrebinaire  B
Variables
   arbrebinaire  Aux
Début
   Aux $\leftarrow$ d(B)		/* Affectations des différents liens */
   d(B) $\leftarrow$ g(Aux)
   g(Aux) $\leftarrow$ B
   B $\leftarrow$ Aux
fin algorithme procédure Rg

Algorithme (Procédure rd)

algorithme procédure Rd
Paramètres globaux
   arbrebinaire  B
Variables
   arbrebinaire  Aux
Début
   Aux $\leftarrow$ g(B)		/* Affectations des différents liens */
   g(B) $\leftarrow$ d(Aux)
   d(Aux) $\leftarrow$ B
   B $\leftarrow$ Aux
fin algorithme procédure Rd

Algorithme (Procédure rgd)

algorithme procédure Rgd
Paramètres globaux
   arbrebinaire  B
Variables
   arbrebinaire  Aux
Début
   Rg(g(B))		/* Appel des rotations simples */
   Rd(B)
fin algorithme procédure Rgd

Algorithme (Procédure rdg)

algorithme procédure Rdg
Paramètres globaux
   arbrebinaire  B
Variables
   arbrebinaire  Aux
Début
   Rd(d(B))		/* Appel des rotations simples */
   Rg(B)
fin algorithme procédure Rdg

Remarques :

• Comme on peut le constater, les rotations doubles sont la combinaison de deux rotations simples. La rotation gauche-droite (droite-gauche) est composée d’une rotation gauche (droite) sur le sous-arbre gauche (sous-arbre droit) de B suivie d’une rotation droite (gauche) sur B. Ces deux fonctions sont optimisables en remplaçant les deux appels de fonction par les affectations adéquates. L’intérêt étant d’éviter les deux appels de fonctions et de réduire le nombre d’affectations de 8 à 6.

• Les rotations conservent la propriété d’arbre binaire de recherche (heureusement, hein ?). On constate, en effet, que la lecture infixe des arbres B, rd(B), rg(B), rgd(B) et rdg(B) est la même.

Les arbres A-V.L.

Les arbres A-V.L. datent des années 60 (1960, pas du temps des Romains et toussa...) et sont la première classe d’arbres H-équilibrés. Leur nom vient de leurs concepteurs (Adelson-Velskii, Landis).

Définitions

• On dit qu’un arbre binaire B = < o, G, D > est H-équilibré si en tout noeud de l’arbre B, les hauteurs des sous-arbres gauche et droit de B différent au plus de 1. C'est à dire si hauteur(G) - hauteur(D) 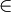$\in$ { -1, 0, +1 }.

• Un arbre AVL est un arbre binaire de recherche H-équilibré.

Spécification formelle

Nous avons alors besoin d'une une opération de déséquilibre, définie récursivement par :

opérations

  déséquilibre : avl $\rightarrow$ entier

axiomes

  déséquilibre(arbrevide) = 0
  déséquilibre(< o, G, D >) = hauteur(G) - hauteur(D)

avec

  avl B, G, D
  noeud        o

Donc, un arbre binaire B est H-équilibré si pour tout sous-arbre C de B on a : Déséquilibre(C) 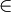$\in$ { -1, 0, 1 }

Nous pouvons voir sur la figure 14.a un exemple d’arbres H-équilibrés, et sur la figure 14.b l’exemple d’un arbre qui ne l’est pas.

Figure 14. Exemples d'arbres binaires H-équilibrés ou non.

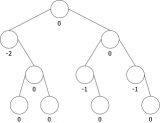
(a) arbres binaires H-équilibrés	(b) arbre binaire non H-équilibré

Nous ne détaillerons pas l’algorithme de recherche dans les AVL. Dans la mesure où ceux-ci sont des arbres binaires de recherche, il suffit de reprendre ceux de la recherche dans un ABR. Le nombre de comparaisons est toujours d’ordre logarithmique.

En revanche, l’ajout ou la suppression dans un AVL peut provoquer un déséquilibre qui générera alors une réorganisation locale ou complète de l’arbre. Nous allons donc étudier (enfin on va essayer) les algorithmes d’ajout et de suppression dans les AVL.

Ajout dans un AVL

Le principe de construction d’un AVL est le suivant: on fait l’ajout du nouvel élément aux feuilles. Puis on rééquilibre l’arbre si cet ajout l’a déséquilibré. Dans ce cas, le déséquilibre maximum que l’on peut rencontrer est ± 2.

Lorsqu’il y a déséquilibre après l’ajout d’un noeud x, il suffit de rééquilibrer l’arbre à partir d’un noeud y se trouvant dans le chemin de la racine à la feuille x (y peut être la racine elle-même). Ce noeud y est le dernier noeud rencontré (le plus proche de x) pour lequel le déséquilibre est ± 2.

Principe général de rééquilibrage

Soit B = < r, G, D > B un AVL , donc n’ayant pas de sous-arbres en déséquilibre ± 2. Supposons que l’on ajoute un élément x sur une feuille de G et que la hauteur de ce dernier augmente de 1 et que G reste un AVL (avant l’ajout dans G, son déséquilibre était 0). Dans ce cas, nous avons les trois possibilités suivantes :

1. Si le déséquilibre de B valait 0 avant l’ajout, il vaut 1 après. B reste un AVL et sa hauteur a augmenté de 1.
2. Si le déséquilibre de B valait –1 avant l’ajout, il vaut 0 après. B reste un AVL et sa hauteur n’est pas modifiée.
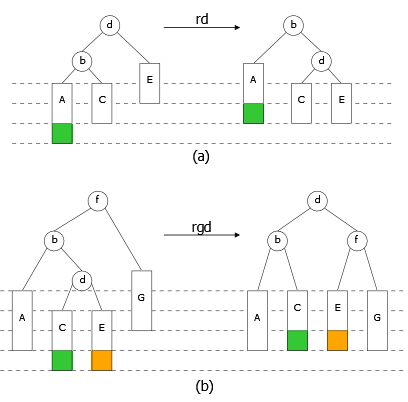
3. Si le déséquilibre de B valait 1 avant l’ajout, il vaut 2 après. B n’est plus H-équilibré, il faut le réorganiser (cf. figure 15).

Figure 15. Ajout dans un AVL (principe de rééquilibrage).

Comme on peut le voir sur la Figure 15, le troisième cas présente deux possibilités :

1. Le déséquilibre de G passe de 0 à 1 (Figure 15(a)) et le rééquilibrage de B se fait à l’aide d’une rotation simple à droite.
2. Le déséquilibre de G passe de 0 à –1, il y a inversion du sens de déséquilibre entre B et G. Dans ce cas, le rééquilibrage s’effectue à l’aide d’une rotation double gauche-droite (Figure 15(b)).

Dans les deux cas, on récupère un arbre B rééquilibré qui est bien un AVL et dont la hauteur est redevenue celle qu’il avait avant l’ajout dé l’élément x (magnifique !).

Remarque: Bien évidemment il existe les trois cas symétriques dans le cas où l’ajout se fasse sur D.

Spécification formelle

Pour l’ajout dans un AVL, nous avons besoin d’une opération ajouter-AVL et de deux opérations gérant le déséquilibre, à savoir rééquilibrer et déséquilibre. La première rééquilibre l’arbre, la deuxième permet de connaître le déséquilibre d’un arbre. Ces opérations sont définies de la manière suivante :

opérations

   ajouteravl  : element x avl $\rightarrow$ avl
   rééquilibrer : avl $\rightarrow$ avl
   déséquilibre : avl $\rightarrow$ entier

préconditions

   rééquilibrer(B) est-défini-ssi déséquilibre(B) $\in$ {-2,-1,0,1,2}

axiomes

   Ajouteravl( x, arbrevide ) = x
   x <= r => ajouteravl( x, < r, G, D >))= rééquilibrer(< r, ajouteravl( x, G), D >)
   x > r => ajouteravl( x, < r, G, D >))= rééquilibrer(< r, G, ajouteravl( x, D)>)
   déséquilibre(B) = -1 => rééquilibrer(B) = B
   déséquilibre(B) =  0 => rééquilibrer(B) = B
   déséquilibre(B) =  1 => rééquilibrer(B) = B
   déséquilibre(B) =  2 & déséquilibre(G) =  1 => rééquilibrer(B) = rd(B)
   déséquilibre(B) =  2 & déséquilibre(G) = -1 => rééquilibrer(B) = rgd(B)
   déséquilibre(B) = -2 & déséquilibre(D) =  1 => rééquilibrer(B) = rdg(B)
   déséquilibre(B) = -2 & déséquilibre(D) = -1 => rééquilibrer(B) = rg(B)

avec

   avl B, G, D
   noeud r
   element x

Remarque: On peut noter qu’il y a au plus un rééquilibrage à chaque ajout.

Algorithme

En terme d’implémentation, nous devons mémoriser dans chaque noeud la valeur de déséquilibre de l’arbre dont il est racine. Il est donc nécessaire de rajouter un champ deseq prenant les valeurs {-2,-1,0,1,2} dans l’enregistrement de type t_noeud défini pour la représentation dynamique des arbres binaires. Ce qui donne :

Types

   t_element = ...                /* Définition du type des éléments */
   t_avl = $\uparrow$t_noeud               /* Définition du type t_arbre (pointeur sur t_noeud) */
   t_noeud = enregistrement       /* Définition du type t_noeud */
      entier    deseq
      t_element elt
      t_avl     fg, fd
   fin enregistrement t_noeud

Variables

   t_avl B

Remarque: Nous allons rester dans un formalisme abstrait, et pour cela nous utiliserons le type Avl qui est un dérivé du type ArbreBinaire auquel nous avons ajouté les opérations propres aux Avl , en détaillant toutefois certaines d’entre elles comme rééquilibrer.

algorithme procédure ajouterAVL
paramètres globaux
   avl	B
paramètres locaux
   element x
variables
   avl	Y, A, AA, P, PP
Début
   Y $\leftarrow$ < 0, x, arbrevide, arbrevide >      /* Création du noeud, deseq = 0 */
   si B = arbrevide alors
      B $\leftarrow$ Y
   sinon
      A $\leftarrow$ B, AA $\leftarrow$ arbrevide              /* AA est le père de A */
      P $\leftarrow$ B, PP $\leftarrow$ arbrevide              /* PP est le père de P */
      tant que P <> arbrevide faire             /* Recherche de la feuille d’ajout */
         si déséquilibre(P) <> 0 alors          /* Si un noeud a un déséquilibre */
            A $\leftarrow$ P                             /* différent de 0, on le mémorise */
            AA $\leftarrow$ PP                           /* dans A, et son père dans AA  */
         fin si
         PP $\leftarrow$ P
         si x <= contenu(racine(P)) alors
            P $\leftarrow$ g(P)
         sinon
            P $\leftarrow$ d(P)
         fin si
      fin tant que
      si x <= Contenu(racine(PP)) alors                 /* Ajout du noeud Y */
         g(PP) $\leftarrow$ Y
      sinon
         d(PP) $\leftarrow$ Y
      fin si
      P $\leftarrow$ A                                           /* Modification du déséquilibre */
      tant que P <> Y faire                             /* sur le chemin de A vers Y      */
         si x <= Contenu(racine(P)) alors
            déséquilibre(P) $\leftarrow$ déséquilibre(P) + 1
            P $\leftarrow$ g(P)
         sinon
            déséquilibre(P) $\leftarrow$ déséquilibre(P) - 1
            P $\leftarrow$ d(P)
         fin si
      fin tant que
      selon les valeurs de déséquilibre(A) faire                          /* Rééquilibrage */
         0, 1, -1 : retourne                                              /* Quitte l’ajout */
                2 : si déséquilibre(g(A)) = 1 alors                       /* Déséquilibre Gauche */
                       rd(A)                                              /* Rotation droite */
                       déséquilibre(A) $\leftarrow$ 0
                       déséquilibre(d(A)) $\leftarrow$ 0
                    sinon
                       rgd(A)                                             /* Rotation gauche-droite */
                       selon les valeurs de déséquilibre(A) faire
                          -1 : déséquilibre(g(A)) $\leftarrow$ 1
                               déséquilibre(d(A)) $\leftarrow$ 0
                           1 : déséquilibre(g(A)) $\leftarrow$ 0
                               déséquilibre(d(A)) $\leftarrow$ -1
                           0 : déséquilibre(g(A)) $\leftarrow$ 0                   /* A=Y */
                               déséquilibre(d(A)) $\leftarrow$ 0
                       fin selon
                       déséquilibre(A) $\leftarrow$ 0
                    fin si
               -2 : si déséquilibre(d(A)) = -1 alors                     /* Déséquilibre Droit */
                       rg(A)                                             /* Rotation gauche */
                       déséquilibre(A) $\leftarrow$ 0
                       déséquilibre(d(A)) $\leftarrow$ 0
                    sinon
                       rdg(A)                                            /* Rotation droite-gauche */
                       selon les valeurs de déséquilibre(A) faire
                          -1 : déséquilibre(g(A)) $\leftarrow$ 0
                               déséquilibre(d(A)) $\leftarrow$ -1
                           1 : déséquilibre(g(A)) $\leftarrow$ 1
                               déséquilibre(d(A)) $\leftarrow$ 0
                           0 : déséquilibre(g(A)) $\leftarrow$ 0                  /* A=Y */
                               déséquilibre(d(A)) $\leftarrow$ 0
                       fin selon
                       déséquilibre(A) $\leftarrow$ 0
                    fin si
      fin selon
      si AA = arbrevide alors		/* Mise à jour des liens */
         B $\leftarrow$ A
      sinon
         si Contenu(racine(A)) <= Contenu(racine(AA)) alors
            g(AA) $\leftarrow$ A
         sinon	
            d(AA) $\leftarrow$ A
         fin si
      fin si
   fin si
fin algorithme procédure ajouterAVL

Remarque: L’utilité du débranchement (et là, je m’adresse à certains correcteurs de ce poly…), pour un déséquilibre de {0,1,-1}, est nécessaire pour éviter la mise à jour des pointeurs en sortie. Cela permet d’éviter un test supplémentaire à la fin (on ne va quand même pas en rajouter, c’est suffisamment pénible comme ça !).

Supprimer dans un AVL

Le principe de suppression d’un élément dans un AVL est le même que dans un arbre binaire. C’est à dire recherche de l’élément à supprimer, suppression et remplacement, le cas échéant, par l’élément qui lui est immédiatement inférieur. Le problème est que cet arbre n’est plus forcément H-équilibré. Il faut donc le rééquilibrer . Après la première phase de suppression, la hauteur de l’arbre est diminuée de 1. S’il y a déséquilibre, la rotation appliquée peut diminuer à son tour la hauteur de l’arbre et générer, éventuellement un nouveau déséquilibre. En fait les rotations peuvent s’enchaîner en cascade depuis l’élément supprimé jusqu’à la racine de l’arbre. Nous devons donc connaître ce chemin. Cela implique l’utilisation d’une pile sur une version itérative de l’algorithme. En fait le principe est simple, si l’on supprime un noeud x, on examine la hauteur de l’arbre de racine x. Si cette hauteur a diminué de 1, il faut éventuellement faire une rotation au niveau du père de 'x. Et ainsi de suite…

Spécification formelle

Pour supprimer dans un AVL, nous avons besoin des opérations « rééquilibre » (définie sur l’ajout AVL), de « Max » et « Suppmax » (définies dans la suppression ABR) et de « Supprimer-AVL » que nous allons définir, soit :

opérations

   supprimeravl  : element x avl $\rightarrow$ avl
   max : avl $\rightarrow$ element
   suppmax : avl $\rightarrow$ avl

préconditions

   max(B) est-défini-ssi B <> arbrevide
   suppmax(B) est-défini-ssi B <> arbrevide

axiomes

   supprimeravl( x, arbrevide) = arbrevide
   x = r => supprimeravl( x, < r, G, arbrevide >)) = G
   x = r & D <> arbrevide => supprimeravl( x, < r, arbrevide, D >)) = D
   x = r & G <> arbrevide & D <> arbrevide
         => supprimeravl( x, < r, G, D >)) = rééquilibrer(< Max(G), suppmax(G), D >)
   x < r => supprimeravl( x, < r, G, D >)) = rééquilibrer(< r, supprimeravl( x, G), D >)
   x > r => supprimeravl( x, < r, G, D >)) = rééquilibrer(< r, G, supprimeravl( x, D) >)
   D <> arbrevide => max(< r, G, D >) = max(D)
   D <> arbrevide => suppmax(< r, G, D >)= rééquilibrer(< r, G, suppmax(D) >)

avec

   avl B, G, D
   noeud r
   element x

Remarque: On peut noter qu’il peut y avoir plus d’un rééquilibrage à chaque suppression.

Algorithme

L’algorithme de suppression faisant l’objet d’un exercice, il n’est pas fourni dans le présent polycopié. Je sais c’est un peu facile. Mais bon, personne ne le fournit, je ne vois pas pourquoi je le ferais. De plus, je m’attirerais alors l’inimitié de certains collègues (dont je tairais les noms) qui se retrouveraient, du coup, avec un exercice de moins en TD.

Les arbres 2.3.4

Nous avons vu que pour éviter la dégénérescence de l’arbre, il existait les arbres binaires H-équilibrés, une autre possibilité est de multiplier les axes de recherche à partir d’un noeud. Dans ce cas, il nous faut utiliser des arbres de recherche. L’arbre 2.3.4 en est un. Ses noeuds peuvent contenir 1, 2 ou 3 éléments et toutes ses feuilles sont situées au même niveau. La hauteur de l’arbre est alors toujours une fonction logarithmique du nombre d’éléments qu’il contient. Il existe des fonctions de rééquilibrage de l’arbre, utilisées éventuellement après chaque ajout ou suppression d’un élément de l’arbre. Toutes les opérations sur les arbres 2.3.4 sont au pire logarithmique.

Définitions

Un arbre de recherche est un arbre général étiqueté dont chaque noeud contient un k-uplet d’éléments distincts et ordonnés (k = 1, 2, 3, ...). Un noeud contenant les éléments x₁ < x₂ < ... < x_k possède k + 1 sous-arbres, tels que :

• Tous les éléments du premier sous-arbre sont inférieurs ou égaux à x₁
• Tous les éléments du i^ème sous-arbre (i = 2, ..., k) sont strictement supérieurs à x_{i - 1} et inférieurs ou égaux à x_i
• Tous les éléments du (k + 1)^ème sous-arbre sont strictement supérieurs à x_k

Dans un arbre de recherche, on appelle k-noeud un noeud contenant (k - 1) éléments.

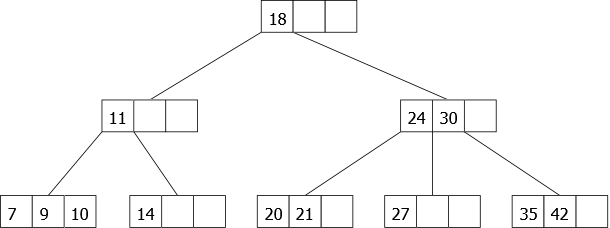
Un arbre 2.3.4 est un arbre de recherche dont les noeuds sont de trois types : 2-noeud, 3-noeud ou 4-noeud et dont toutes les feuilles sont situées au même niveau.

Figure 16. Exemple d'arbre 2.3.4

Comme nous pouvons le constater sur la figure 16, nous avons un exemple d’arbre 2.3.4 contenant 13 éléments distincts et constitué de 8 noeuds. Les éléments à l’intérieur de chaque noeud sont rangés en ordre croissant et toutes les feuilles de l’arbre se situent au même niveau.

Recherche dans un Arbre 2.3.4

La recherche d’un élément x dans un arbre 2.3.4 A fonctionne globalement de la même manière que pour la recherche dans un ABR, le principe est le suivant :

On compare x avec l’élément ou les éléments x₁, _..., x_i (i = 1, 2 ou 3) contenus dans le noeud racine de A , dans ce cas plusieurs possibilités :

• s’il existe j $\in$ [1,i] tel que x = x_j, alors on a trouvé x et la recherche s’arrête (recherche positive)

• si x < x₁, la recherche de x se poursuit dans le 1^er sous-arbre de A

• si x_j < x < x_{j + 1} (j = 1, ..., i - 1), la recherche de x se poursuit dans le (j + 1)^ème sous-arbre de A

• si x > x_i, la recherche de x se poursuit dans le dernier sous-arbre de A

• si la recherche se termine sur une feuille ne contenant pas x, alors x n’existe pas dans A (recherche négative)

Remarque: La recherche d’un élément dans un arbre 2.3.4 suit un chemin de la racine vers une feuille. La hauteur de l’arbre étant fonction logarithmique du nombre d’élément, la complexité de l’algorithme de recherche en nombre de comparaisons entre éléments, est toujours logarithmique.

Ajout dans un arbre 2.3.4

Nous allons étudier l’ajout aux feuilles. Le seul problème posé par ce dernier se présente si la feuille qui doit recevoir le nouvel élément est un 4-noeud (le noeud est déjà plein). Dans ce cas, il va falloir ajouter un nouveau noeud et rééquilibrer l’arbre. C’est une fonction d’éclatement qui permet cela. L’éclatement des 4-noeuds peut se faire :

• soit en descendant le long du chemin à la recherche de la feuille d’ajout,
• soit en remontant (algorithme implicitement récursif).

Ajout avec éclatements à la remontée

Nous allons présenter un exemple d’ajouts successifs aux feuilles qui montre l’évolution de l’arbre. Nous utiliserons successivement les éléments suivants : 30, 11, 35, 18, 27, 42, 14, 10, 24, 7, 21, 9, 20.

L’ajout de 30 crée un 2-noeud qui se transforme en 3-noeud lors de l’ajout de 11 puis en 4-noeud pour 35, ce qui donne l’évolution présentée figure 17.

Figure 17. Ajout de 30, 11 et 35 dans un arbre 2.3.4

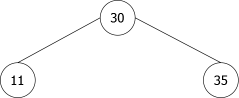
A ce stade, l’ajout d’un élément est impossible, l’unique feuille est un 4-noeud. Le noeud unique pourrait être assimilé à l’arbre binaire de la figure 18. Pour pouvoir ajouter un élément, nous allons devoir "éclater" le noeud en créant deux 2-noeuds contenant respectivement le plus petit et le plus grand élément du noeud éclaté.

• Si le noeud éclaté est racine de l’arbre, nous créons un noeud supplémentaire et la hauteur de l’arbre augmente de 1.
• Si le noeud éclaté n’est pas racine, l’élément central remonte vers le noeud père et s’y insère.

Figure 18. ABR équivalent à l'arbre 2.3.4 de la figure 17

On reprend donc cet arbre qui est bien un arbre 2.3.4 et l’on ajoute 18, 27 et 42, ce qui donne l’arbre 2.3.4 de la figure 19.

Figure 19. Ajout de 18, 27 et 42 dans l'arbre 2.3.4

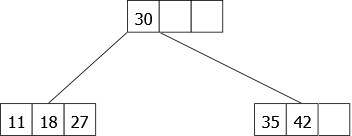
L’ajout de 14 devrait se faire dans la première feuille, mais celle-ci est pleine. Nous devons donc l’éclater. Celle-ci n’étant pas une racine, l’élément central (18) va remonter vers le noeud père et s’insérer naturellement (enfin, c’est une façon d’écrire) à sa place. Nous obtiendrons alors une nouvelle feuille dans laquelle l’élément 14 va pouvoir s’insérer. Ensuite, nous ajoutons 10 et 24, ce qui donne l’arbre en figure 20.

Figure 20. Ajout de 14, 10 et 24 dans l'arbre 2.3.4

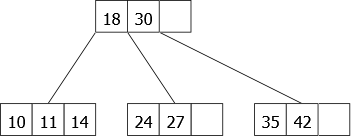
L’ajout du 7 éclate le première feuille en générant la remontée du 11 vers la racine qui devient alors un 4-noeud. Ensuite, on ajoute le 21 et le 9. On obtient alors l’arbre 2.3.4 de la figure 21.

Figure 21. Ajout de 7, 21 et 9 dans l'arbre 2.3.4

Enfin, on ajoute le 20. Celui-ci devrait se trouver dans la troisième feuille qui nécessite un éclatement. Or, la remontée du 24 ne peut se faire dans la mesure ou son noeud père (la racine) est aussi un 4-noeud. Dans ce cas, lui aussi sera éclaté et la hauteur de l’arbre va augmenter de 1. Ce qui donne l’arbre de la figure 22.

Figure 22. Ajout pour finir de 20 dans l'arbre 2.3.4

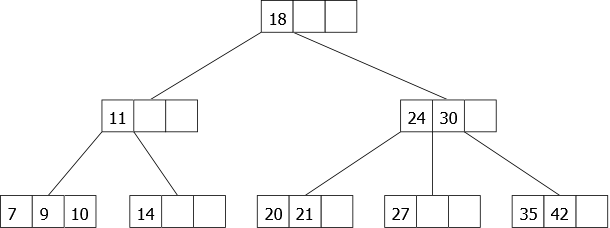
Ajout avec éclatements à la descente

Nous n’allons pas présenter l’ajout avec éclatement à la descente, mais faire simplement quelques remarques. Son but est d’éviter les cascades d’éclatement comme générées par l’ajout du 20 (figure 22).En effet, lorsque l’on parcourt l’arbre à la recherche de la feuille dans laquelle doit s’effectuer l’ajout, nous éclatons systématiquement chaque 4-noeud rencontré. Dès lors, il ne peut pas y en avoir deux consécutifs (eh oui ! Je vous laisse réfléchir.). L’avantage de cette méthode est que l’on peut écrire une version itérative de l’algorithme sans utiliser de pile dans la mesure où nous n’avons pas besoin de mémoriser le chemin de la racine à la feuille que l’on crée. L’inconvénient est d’augmenter inutilement la hauteur de l’arbre (par éclatement de la racine) comme il aurait pu se produire à la figure 21 si nous avions ajouté la valeur 13 ; Ce qui ne nécessitait pas l’éclatement de la racine dans le cas d’un ajout à la remontée.

Remarque: Les deux méthodes opérant sur un chemin allant de la racine à la feuille dans laquelle doit se faire l’ajout, leur complexité est dans tous les cas fonction logarithmique du nombre d’éléments de l’arbre.

Remarque 2: Dans le cas de redondance de valeurs, deux éléments de même valeur pourraient à la suite d’éclatements se trouver dans des noeuds différents. Nous ne traitons pas ces cas particuliers. En effet, les éléments d’un noeud fils pourraient ne pas être strictement supérieurs à celui du noeud père. Dans ce cas une modification de la définition des arbres 2.3.4 ainsi que des algorithmes de recherche et d’ajout serait nécessaire.

Suppression dans un arbre 2.3.4.

Quels sont les problèmes posés par la suppression d'un élément dans un arbre 2.3.4.?

• Comme dans tout arbre, la suppression d’un noeud interne dans un arbre 2.3.4. pose un problème: cela crée des orphelins! Il est donc plus simple de supprimer un élément dans une feuille. Lorsque l'élément à supprimer est dans un noeud interne, on utilisera la méthode habituelle: on remplace celui-ci par son immédiat inférieur (l'élément maximum de son fils gauche), c'est à dire le dernier élément de la feuille la plus à droite ou alors par son immédiat supérieur (l'élément minimum de son fils droit), c'est à dire le premier élément de la feuille la plus à gauche. Nous verrons plus loin ce qui justifiera l’utilisation de l’une ou l’autre de ces deux possibilités.

Ainsi on se ramène toujours à la suppression d’une feuille!

• La suppression d’un élément dans une feuille d’un arbre 2.3.4. pose un problème lorsque l’on est sur un 2-noeud. Supprimer l'élément unique reviendrait à détruire la feuille, l’arbre n’est donc plus un arbre 2.3.4. (dont, on le rappelle, toutes les feuilles doivent être au même niveau).

Quelles sont alors les solutions possibles ?

Tout comme il est impossible d’insérer un élément dans un 4-noeud, il est impossible de supprimer un élément dans un 2-noeud. La solution sera donc similaire à celle vue pour l’insertion: le problème de l’insertion était résolu en déplaçant des éléments dans les noeuds ”voisins” pour faire de la place pour le nouvel élément. Pour la suppression, il faudra trouver des éléments supplémentaires pour le noeud concerné.

L’idée est de faire descendre un élément du noeud père. Même si la suppression effective se fera toujours dans une feuille, nous verrons plus loin que les transformations décrites ici devront être utilisées pour tout type noeud. Deux transformations seront utilisées (soit i le numéro du fils ne contenant qu’un seul élément):

• Les rotations

L'élément du père qui descend est remplacé par un élément d’un des frères du noeud. Le frère en question doit donc contenir au moins deux éléments!

– Si le fils i-1 (le frère gauche) contient au moins deux éléments : le plus grand remonte dans le père à la position i-1. L'élément i-1 du père descend alors dans le fils i, qui n’est plus un 2-noeud. C’est la rotation droite (voir figure 22.1). Le fils droit de l'élément ”remonté“ devient fils gauche de l'élément ”descendu“.

– Symétriquement, si le fils i+1 (le frère droit) contient au moins deux éléments: le plus petit remonte dans le père à la position i. L'élément numéro i du père descend alors dans le fils i, qui n’est plus un 2-noeud. C’est la rotation gauche. Le fils gauche de l'élément ”remonté“ devient fils droit de l'élément ”descendu“.

Figure 22.1 Rotation droite du fils i-1 vers le fils i

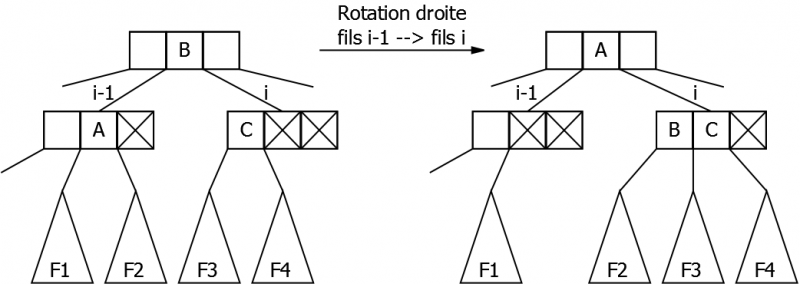
• La fusion (voir figure 22.2)

Utiliser une rotation nécessite d’avoir un des frères qui ne soit pas un 2-noeud. Lorsque ce n’est pas le cas, on va appliquer une transformation ”inverse” de celle de l’éclatement: l’éclatement était nécessaire lorsqu’il y avait une occupation maximum des noeuds, ce qui empêchait toute insertion. Ici nous nous retrouvons avec une occupation minimum des noeuds : le fils i et ses deux frères (s’ils existent) sont des 2-noeuds. La solution est de diminuer le nombre de noeuds, en regroupant deux 2-noeuds en un seul. C’est la fusion, dont le principe est le suivant:

Le fils i et le fils i+1 (s’il existe, sinon on peut faire de même avec le fils i-1), sont regroupés en un seul noeud. Dans le noeud père il y a donc un élément de trop : celui dont les deux fils ont fusionné. On descend donc cet élément dans le noeud fusionné dont il devient l'élément médian. Les deux éléments des fils ”emmènent“ leurs fils avec eux.

Figure 22.2 Fusion du fils i et du fils i+1

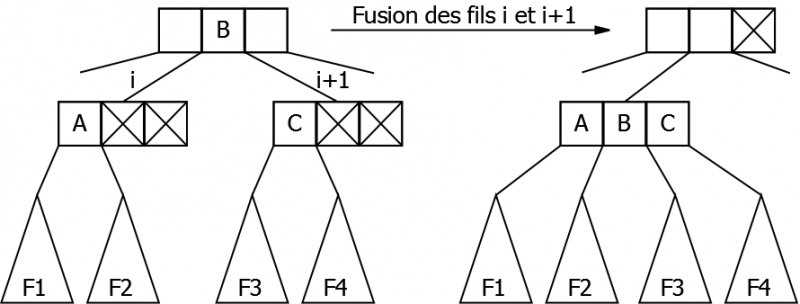
Il est important de noter que la fusion ne pourra être appliquée que si le noeud père n’est pas un 2-noeud.

Les transformations présentées ici nécessitent toutes deux l’intervention du noeud père: la transformation d’un 2-noeud se fera donc avant de descendre sur celui-ci; le cas de la racine devenant alors un cas particulier.

Principe de suppression dans un arbre 2.3.4.

Résumons:

• La suppression d’un élément dans un arbre 2.3.4. se fera toujours dans une feuille : si l'élément cherché est dans un noeud interne, il suffit de la remplacer par le maximum de son fils gauche, ou le minimum de son fils droit (qui sont tous deux dans une feuille).

• Si le noeud dans lequel on supprime est un 2-noeud, il suffit de faire migrer un élément d’un de ses frères (par une rotation) ou de faire une fusion avec l’un de ses frères.

Problème!

Effectuer une rotation n’est pas possible lorsque les frères du noeud sont des 2-noeuds (ou l’unique frère, si on est sur un ”bord“). La solution est donc la fusion. Cette transformation nécessite que le noeud père ne soit pas un 2-noeud. Que faire si c’est le cas ?

On se retrouve ici, une fois de plus, face à un problème similaire à celui de l’insertion! Une première solution consisterait à transformer à son tour le père afin qu’il contienne au moins deux éléments. Mais si le père de celui-ci est un 2-noeud, on peut se retrouver face au même problème. Tout comme la solution d’éclatement à la remontée, les transformations peuvent se propager jusqu’à la racine.

La solution:

Nous allons donc appliquer de nouveau le principe de précaution : les transformations se feront à la descente dès que l’on rencontrera un 2-noeud. On est ainsi sûr de ne jamais avoir deux 2-noeuds ui se suivent, et arrivé sur la feuille, la suppression se fera sans aucun problème.

Ce principe de précaution implique un choix quant au remplacement de l'élément à supprimer lorsque celui-ci est dans un noeud interne: on choisira le maximum du fils gauche si celui-ci n’est pas un 2-noeud; sinon c’est le minimum du fils droit qui sera utilisé. Mais si les deux fils sont des 2-noeuds, alors la solution sera de les fusionner (dans ce cas, l'élément à supprimer descendra d’un niveau).

Le principe:

Soient A un arbre 2.3.4. et x l'élément à supprimer. Lors du parcours de A à la recherche de la clé x, il est nécessaire de toujours s’assurer que le noeud vers lequel on descend comporte au moins deux éléments (ne soit pas un 2-noeud). Le seul noeud autorisé à être un 2-noeud est la racine (nous verrons plus loin que cela ne pose pas de problème)! D’ailleurs, il faut traiter la racine à part dans une première procédure comme pour l’insertion (celle-ci se chargera aussi du cas de l’arbre vide ou de l’arbre réduit à une feuille).

L’algorithme sera récursif. A chaque étape, nous sommes donc sur un arbre non vide, dont la racine contient au moins deux éléments (sauf éventuellement la racine de l’arbre initial).

La première chose à faire est de rechercher la ”position“ de l'élément dans le noeud courant. Soit i cette position : i désigne le numéro de l'élément recherché si celui-ci est présent, le numéro du fils où descendre sinon. Examinons tous les cas:

• Soit x n'est pas dans le noeud courant:

Le noeud courant est un noeud interne:

Le noeud courant est une feuille:

Si ce fils i est un 2-noeud, il faut le modifier pour augmenter le nombre de ses clés: Soit le frère gauche, le fils i-1 (s’il existe) est au moins un 3-noeud, on applique une rotation droite. Soit le frère droit, le fils i+1 (s’il existe) est au moins un 3-noeud, on applique une rotation gauche. Sinon on procède à une fusion, avec le frère droit (i+1) s’il existe, le gauche (i-1) sinon. → On relance la suppression sur le fils i (le fils i-1 dans le cas d'une fusion avec le frère gauche) qui n'est pas un 2-noeud.

La clé n’est pas dans l’arbre. → l'algorithme s'arrête.

• Soit x est dans le noeud courant:

Le noeud courant est un noeud interne:

Le noeud courant est une feuille:

Il faut remplacer, si cela est possible, l'élément x par un élément se trouvant dans une feuille: – Soit le fils gauche de l'élément x est au moins un 3-noeud, et dans ce cas, on remplace l'élément x par le maximum de son sous-arbre gauche → on relance la suppression du maximum sur le sous-arbre gauche. – Soit le fils droit de l'élément x est au moins un 3-noeud, dans ce cas, on remplace l'élément x par le minimum de son sous-arbre droit → on relance la suppression du minimum sur le sous-arbre droit. – Sinon, on fait une fusion sur l'élément x → on relance la suppression de l'élément x sur le fils résultant de la fusion.

Ce noeud comporte forcément 2 éléments → on supprime l'élément x directement.

Application du principe:

Arbre d'origine:

Figure 22.3 Suppression: Arbre 2.3.4. d'origine

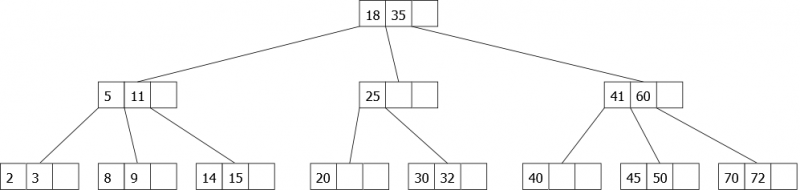
Suppression de l'élément 32: Avant de descendre sur le noeud {25}, on fait une rotation droite (l'élément 11 remonte dans le noeud père, l'élément 18 descend dans notre noeud. On descend jusqu'à 32 que l’on supprime.

Figure 22.4 Suppression de l'élément 32

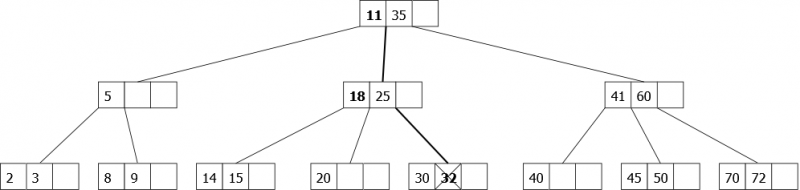
Suppression de l'élément 25: Les fils gauche et droit de 25 sont des 2-noeuds, on fait donc descendre cet élément en fusionnant ces deux fils. 25 est alors supprimé dans la feuille résultat de la fusion.

Figure 22.5 Suppression de l'élément 25

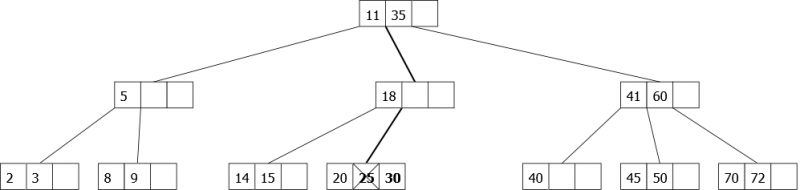
Suppression de la clé 35: 35 est dans le noeud racine : on le remplace par le plus petit élément de son fils droit (qui n’est pas un 2-noeud). Puis on relance la suppression de cet élément: 40. Le noeud qui contient 40 est un 2-noeud, on fait une rotation gauche avant d’y descendre pour supprimer l'élément.

Figure 22.6 Suppression de l'élément 35

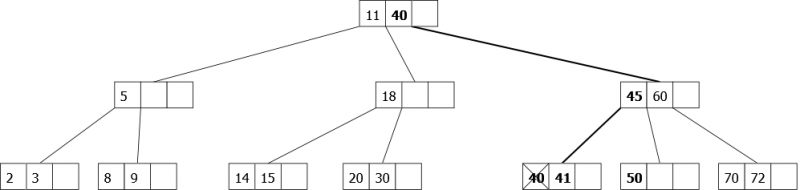
Suppression de l'élément 5: 5 est dans le premier fils qui est un 2-noeud. Aucune rotation n'est possible puisque le frère droit est aussi un 2-noeud. On fait donc d’abord une fusion entre les deux premiers fils, puis on descend sur le noeud résultat contenant 5 que l’on remplace par le maximum de son fils gauche, que l’on supprime.

Figure 22.7 Suppression de l'élément 5

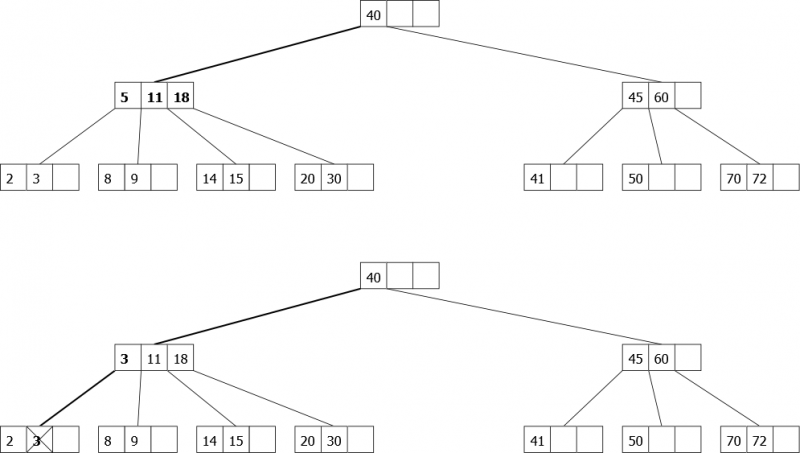
Représentation des arbres 2.3.4

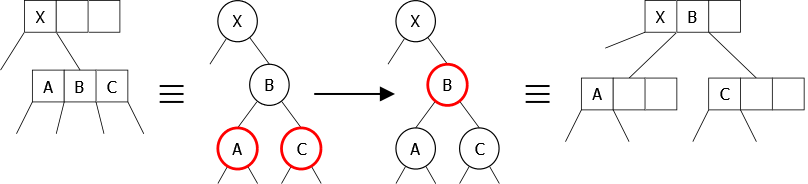
Le passage à l’implémentation peut se faire de différentes manières, la première consiste à créer la structure propre à chaque noeud comme montré sur la figure 23.

Figure 23. Représentation séparée des 2-Noeud, 3-Noeud et 4-Noeud

Ce qui permet de minimiser l’utilisation mémoire, mais qui rend l’implémentation plus complexe, dans la mesure où il est nécessaire de traiter chaque opération pour chaque type de noeud. De plus l’augmentation du nombre de tests ralentira notablement l’exécution.

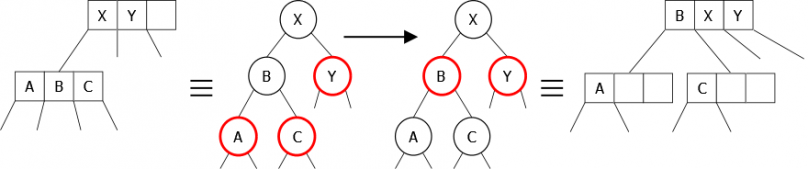
Une autre possibilité est la représentation maximale. C’est à dire que l’on prend le cas maximum (4-Noeud) et l’on utilise cette représentation pour tous les types de noeuds comme montré Figure 24. Dans ce cas, si le noeud est un 2-noeud, nous n’utiliserons que les trois premiers champs de la structure.

Figure 24. Représentation maximale d’un arbre 2.3.4

Le problème, dans ce cas, est le gaspillage de mémoire pour tout ce qui n’est pas 4-noeud. D’autre part, la suppression d’un élément oblige éventuellement le décalage des éléments et des pointeurs sur fils. Une possibilité de simplification est de construire une structure contenant deux tableaux : un de trois éléments et un de quatre pointeurs. Ce qui donnerait :

Constantes

   MaxElt  = 3                    /* Nombre maximum d’éléments */
   MaxFils = MaxElt + 1

Types

   t_element = ...                /* Définition du type des éléments */
   t_a234    = $\uparrow$t_noeud234       /* Définition du type t_a234 (pointeur sur t_noeud234) */
   t_vectElt = MaxElt t_element   /* Tableau d’éléments */
   t_vectFils = MaxFils t_a234    /* Tableau de pointeurs sur fils */
   t_noeud234 = enregistrement
     t_vectElt  elts
     t_vectFils fils
   fin enregistrement t_noeud234

Variables

   t_a234 A

Il existe une troisième forme de représentation des arbres 2.3.4 qui présente l’avantage d’être uniforme et minimale. Ce sont les arbres bicolores.

Arbres bicolores

Les arbres bicolores, inventés par Guibas et Sedgewick, sont des arbres binaires de recherche. Leur particularité tient au fait que leurs noeuds sont soit rouges, soit noirs. Ces arbres sont une représentation des arbres 2.3.4 et ne sont utilisés que dans le but de faciliter l’implémentation de ces derniers.

Dans un arbre 2.3.4, deux éléments appartenant au même noeud sont dits jumeaux. Dans un arbre binaire, les noeuds ne peuvent contenir qu’un seul élément, c’est là qu’intervient la couleur du noeud. Elle permet de distinguer la hiérarchie des éléments entre eux. Si un noeud fils (dans l’arbre bicolore) contient un élément jumeau de celui contenu dans le noeud père, le noeud fils sera rouge. Si ces éléments appartiennent à deux noeuds différents dans l’arbre 2.3.4, le noeud fils (dans l’arbre bicolore) sera noir.

Nous allons présenter les étapes de transformation d’un arbre 2.3.4 en arbre bicolore. Pour un 4-noeud, la transformation est simple comme montré en Figure 25.

Figure 25. Transformation d'un 4-noeud

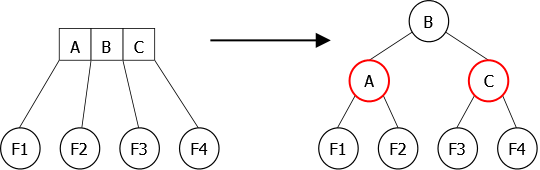
Pour un 3-noeud, il existe deux possibilité. En effet, à la suite d’ajout et de rotation de rééquilibrage, le 3-noeud peut être penché à gauche ou penché à droite comme le montre la Figure 26.

Figure 26. Transformation d'un 3-noeud (penché à gauche ou à droite)

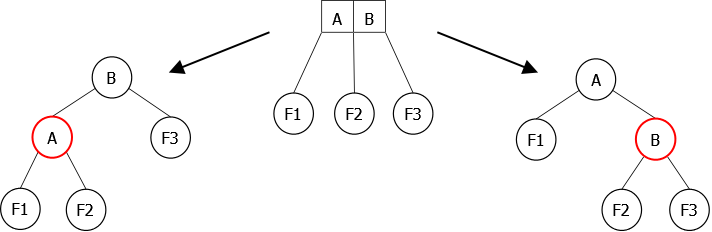
Remarque: Comme il ne peut jamais y avoir deux liens rouges consécutifs (liens vers fils rouge) et que les chemins ont un nombre de liens noirs égal à la hauteur de l’arbre 2.3.4 initial, la hauteur de l’arbre bicolore est au plus égale à deux fois la hauteur de l’arbre 2 .3.4 initial.

Remarque 2: Un arbre bicolore associé à un arbre 2.3.4 de n éléments a une hauteur d’ordre logarithmique.

Figure 27. Arbre bicolore associée à l'arbre 2.3.4 de la figure 16

La figure 27 représente une possibilité d’arbre bicolore associé à celui de la figure 16. En effet, une arrivée de données différente (au vu d’éventuels rééquilibrages) donnerait un autre arbre avec des 3-neouds penchés dans l'autre sens par exemple.

Recherche dans un arbre bicolore

En fait, indépendamment de la couleur des noeuds, c'est un arbre binaire de recherche et la recherche s’effectue à l’aide des algorithmes de recherche sur ABR. Le nombre de comparaisons est donc logarithmique dans le pire des cas.

Ajout dans un arbre bicolore

L’ajout d’un élément peut être réalisé en simulant l’ajout avec éclatement à la descente. L’éclatement d’un 4-noeud revient à inverser les couleurs des nœuds comme le montre la figure 28.

Figure 28. Simulation d’éclatement d’un 4-noeud en représentation bicolore

Cette transformation peut malheureusement faire apparaître des noeuds rouges consécutifs dans l’arbre. Cela a pour conséquence de déséquilibrer l’arbre. Il faut donc le rééquilibrer, et pour cela nous allons utiliser les rotations vu précédemment.

Plusieurs cas peuvent se présenter :

• Le 4-noeud à éclater est attaché à un 2-noeud. Une simple inversion des couleurs suffira (Figure 29).

Figure 29. Eclatement d'un 4-noeud attaché à un 2-noeud

• Le 4-noeud à éclater est attaché à un 3-noeud. Nous considérerons que le 3-noeud est penché à droite, il y alors 3 possibilités :

• • Il est le premier fils du 3-noeud. Il suffit là encore d’inverser les couleurs (Figure 30).

Figure 30. Eclatement d'un 4-noeud attaché au premier fils d'un 3-noeud penché à droite

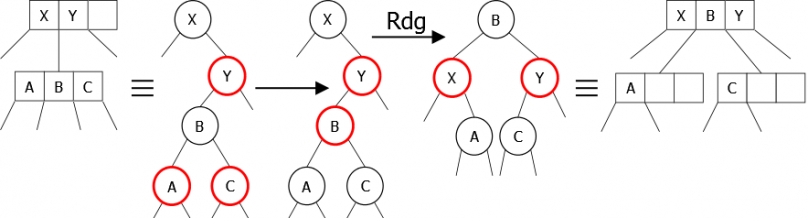
• • Il est le second fils du 3-noeud. L’inversion des couleurs entraîne un déséquilibre, il suffit alors d’effectuer une rotation droite-gauche pour rééquilibrer l’arbre (Figure 31).

Figure 31. Eclatement d'un 4-noeud attaché au second fils d'un 3-noeud penché à droite

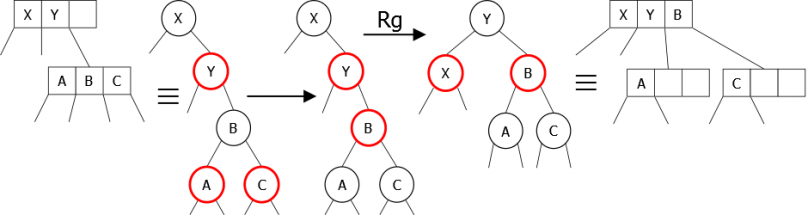
• • Il est le dernier fils du 3-noeud. L’inversion des couleurs entraîne un autre déséquilibre, il suffit alors d’effectuer une rotation gauche pour rééquilibrer l’arbre (Figure 32).

Figure 32. Eclatement d'un 4-noeud attaché au dernier fils d'un 3-noeud penché à droite

Remarque: Il y a, bien évidemment, les trois cas symétriques lorsque le 3-nœud est penché à gauche.

Algorithme

Le principe est simple, nous descendons à partir de la racine à la recherche de la feuille où doit se faire l’ajout du nouvel élément. Sur ce chemin, à chaque fois que l’on rencontre un noeud noir possédant deux fils rouges, nous inversons leur couleur (éclatement du noeud). Dans ce cas, il faut regarder si le père de ce noeud n’est pas rouge auquel cas il est nécessaire d’effectuer la rotation appropriée pour rééquilibrer l’arbre. Une fois l’ajout de l’élément fait , il faut regarder si son père est rouge. Si c’est le cas, une rotation est là aussi nécessaire. En effet, les nouvelles feuilles sont systématiquement rouges dans la mesure où l’on ajouter un élément jumeau.

En terme d’implémentation, nous devons mémoriser dans chaque nœud la couleur de celui-ci. Il est donc nécessaire de rajouter un champ coul prenant les valeurs {Rouge, Noir} dans l’enregistrement de type t_Noeud défini pour la représentation dynamique des arbres binaires. Ce qui donne:

Types

   t_element = ...                /* Définition du type des éléments */
   couleur = (Rouge, Noir)
   t_bic = $\uparrow$t_noeudbic            /* Définition du type t_bic (pointeur sur t_noeudbic) */
   t_noeudbic = enregistrement    /* Définition du type t_noeudbic */
      couleur   coul
      t_element elt
      t_bic     fg, fd
   fin enregistrement t_noeudbic

Variables

   t_bic arbrebic

Remarque: Nous allons rester dans un formalisme abstrait, et pour cela nous utiliserons le type Bic qui est un dérivé du type ArbreBinaire auquel nous avons ajouter les opérations propres aux Arbres Bicolores , Comme couleur nous permettant d’extraire la couleur d’un noeud.

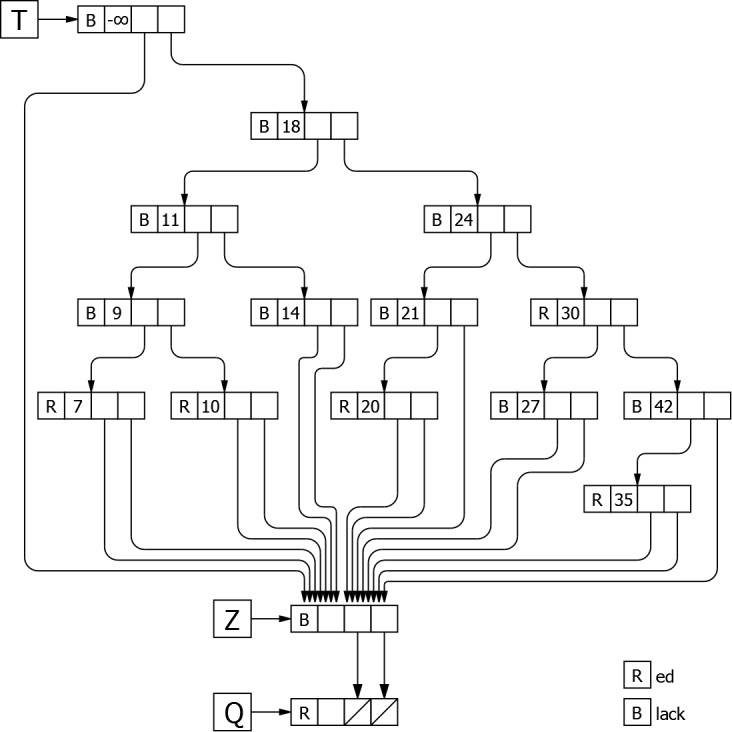
Pour simplifier l’algorithme, la procédure d’ajout utilise un arbre bicolore avec trois éléments supplémentaires ; une tête T, une sentinelle Z et un élément Q pointé par la sentinelle, comme le montre la Figure 33.

La tête T contient un élément dont la valeur est strictement inférieure à toutes celles possibles, sa couleur est le noir, son fils gauche pointe sur la sentinelle Z et son fils droit sur le nœud racine de l’arbre s’il existe. L’intérêt de son utilisation est de supprimer le cas particulier d’un ajout sur arbre vide.

La sentinelle Z est classique. Tous les liens de l’arbre devant pointer vers un arbre vide pointe sur elle. Au début, on lui affecte la valeur à ajouter, ce qui permet de ne pas avoir à tester deux possibilités de sortie de la recherche (arbre vide et l’élément existe déjà). Sa couleur est le noir.

L’élément Q, quant à lui, permet de n’avoir qu’un seul traitement, que l’inversion de couleurs (éclatement) se fasse au milieu de l’arbre où sur la feuille que l’on vient d’ajouter. Sa couleur est le rouge (je ne me permettrai pas de mauvais jeu de mot) et ses deux fils pointent sur un arbre vide.

Figure 33. Représentation (utilisée par l'algorithme d'ajout) de l’arbre bicolore de la Figure 27

algorithme procédure ajouterBIC
paramètres globaux
   bic     T, A
   booléen b
paramètres locaux
   element x
   bic     Z, Q
variables
   bic     P, GP, AGP          /* Mémorisation des trois ascendants */
début
   A $\leftarrow$ T
   Contenu(racine(Z)) $\leftarrow$ x
   b $\leftarrow$ Faux
   P $\leftarrow$ T
   GP $\leftarrow$ T
   faire
      AGP $\leftarrow$ GP
      GP $\leftarrow$ P
      P $\leftarrow$ A
      si x < contenu(racine(A)) alors
         A $\leftarrow$ g(A)
      sinon
         A $\leftarrow$ d(A)
      fin si
      si couleur(g(A)) = Rouge et couleur(d(A))=Rouge alors          /* 2 fils rouges */
         si A = Z alors          /* Ajout */
            b $\leftarrow$ Vrai
            A $\leftarrow$ <Rouge,x,Z,Z>          /* Création du nœud, Coul=Rouge */
            si x < contenu(racine(P)) alors
               g(P) $\leftarrow$ A
            sinon
               d(P) $\leftarrow$ A
            fin si
         sinon
            couleur(A) $\leftarrow$ Rouge)
            couleur(g(A)) $\leftarrow$ Noir
            couleur(d(A)) $\leftarrow$ Noir
         fin si
         si couleur(P) = Rouge alors          /* Rééquilibrage */
            si contenu(racine(P)) > contenu(racine(GP)) alors
               si contenu(racine(A)) > contenu(racine(P)) alors
                  RG(GP)
               sinon
                  RDG(GP)
               fin si
            sinon
               si contenu(racine(A)) > contenu(racine(P)) alors
                  RGD(GP)
               sinon
                  RD(GP)
               fin si
            fin si
            si contenu(racine(AGP)) > contenu(racine(GP)) alors
                g(AGP) $\leftarrow$ GP
            sinon
               d(AGP) $\leftarrow$ GP
            fin si
            couleur(GP) $\leftarrow$ Noir          /* Rétablissement des couleurs */
            couleur(g(GP)) $\leftarrow$ Rouge
            couleur(d(GP)) $\leftarrow$ Rouge
            P $\leftarrow$ GP          /* Rétablissement des hiérarchies */
            GP $\leftarrow$ AGP
            si x = contenu(racine(P)) alors
               A $\leftarrow$ P
            sinon
               si x < contenu(racine(P)) alors
                  A $\leftarrow$ g(P)
               sinon	
                  A $\leftarrow$ d(P)
               fin si
            fin si
         fin si          /* Fin rééquilibrage */
      fin si          /* Fin 2 fils Rouges */
   tant que x <> contenu(racine(A))
   couleur(d(T)) $\leftarrow$ Noir          /* Racine toujours noire */
fin algorithme procédure AjouterBic

Conclusion

En ce qui concerne ces différents types d’arbres de recherche, la complexité des algorithmes de recherche, d’ajout et de suppression est toujours majorée, au pire, par une fonction logarithmique du nombre d’éléments. En ce qui concerne la complexité en moyenne, nous ne possédons, dans de nombreux cas, qu’une valeur expérimentale. Cela dit, il faut tenir compte du coût de réorganisation (éclatement, rotation) pour l’ajout et la suppression. Un des cas extrêmes étant la suppression d’un élément dans un AVL qui peut entraîner jusqu’à 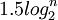$1.5 log_2^n$ rotations.

---

(Christophe "krisboul" Boullay)