Epita:Algo:Cours:Info-Spe:les plus courts chemins

Généralités

Remarques et définitions :

• Nous nous intéresserons aux chemins de longueur non nulle.
• Nous allons travailler sur des graphes orientés valués.
• Le coût (poids ou valeur) d'un chemin est égal à la somme des coûts des arcs qui le composent. On l'appelle aussi la distance du chemin.
• Le plus court chemin d'un sommet x vers un sommet y est le chemin de coût minimum allant de x vers y. Un tel chemin n'existe pas forcément.
• La plus petite distance d'un sommet x vers un sommet y est le coût du plus court chemin s'il existe.

Conditions d'existence:

Considérons un chemin M allant d'un sommet x à un sommet y. Supposons que ce chemin possède un circuit T. Appelons M' le chemin obtenu en retirant T de M, on a alors la relation de coût suivante:

Coût(M) = Coût(M') + Coût(T)

Si le Coût(T) est négatif (<0), il n'existe dans ce cas pas de plus court chemin allant de x à y. En effet, il suffit de repasser une fois de plus par le circuit T pour obtenir un meilleur résultat (chemin de coût inférieur).

Un tel circuit est appelé circuit absorbant.

Si le Coût(T) est nul (=0), M' est de coût égal à celui de M. Dans ce cas c'est aussi un plus court chemin, mais sa longueur (nombre de sommets empruntés) est supérieure à celle de M.

Si le Coût(T) est positif (>0), M' est de coût inférieur à celui de M. Dans ce cas c'est un meilleur candidat que M au titre de plus court chemin.

S'il existe des circuits, ils sont de coût positif ou nul. Or un plus court chemin ne peut pas contenir de circuit de coût strictement positif et s'il existe des circuits de coût nul, il y a plusieurs solutions au problème de la recherche de plus court chemin.

Comme le nombre de chemin élémentaires (ne passant pas plusieurs fois par un même sommet), allant d'un sommet x à un sommet y, est fini, il existe au moins un plus court chemin élémentaire allant de x vers y (note: Il peut en exister plusieurs).

En conclusion: Il existe une solution au problème de la recherche d'un plus court chemin allant de x à y s'il existe un chemin de x à y et s'il n'y a pas de circuit absorbant.

Variantes du problème:

Les algorithmes que nous allons présenter fournissent, dans le cas où il n'y a pas de circuit absorbant, un plus court chemin élémentaire.

Les trois possibilités de rechercher un plus court chemin sont:

1. entre deux sommets x et y,
2. d'un sommet x (une source) vers tous les autres sommets du graphe,
3. entre tous les couples de sommets x et y.

Remarques:

• Le 1) étant obtenu en meilleur solution du 2), nous ne nous intéresserons qu'au 2) et 3).
• Il n'existe pas d'algorithme général que ce soit pour le 2) ou le 3). Il faut tenir compte des propriétés des graphes manipulés et du problème posé et dès lors choisir l'algorithme le plus adapté.

Dijkstra

L'algorithme de Dijkstra n'est utilisable que dans les cas, très fréquents, où les coûts des arcs sont positifs ou nuls. Il détermine le plus court chemin entre un sommet de départ x et tous les autres sommets du graphe accessibles depuis x. On obtient alors un arbre de racine x formé par les plus courts chemins de x vers les sommets qu'il peut atteindre. Il est à noter que n'ayant pas de coûts négatifs, il accepte les graphes présentant des circuits.

Principe

Soit G=< S,A,C > un graphe orienté valué de n sommets. Soit x un sommet de S, on se propose de construire un ensemble CC (court chemin) de sommets y pour lesquels on connait un plus court chemin depuis x.

• Au départ, CC ne contient que la source (x).
• A chaque étape, on ajoute à CC un sommet y pour lequel la plus petite distance (ppdistance(x,y,G)) et le père (pere(x,y,G)) sont connus.
• On s'arrête lorsque CC contient tous les sommets accessibles depuis x.

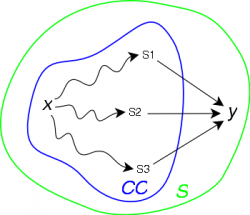
Soit M le complémentaire de CC dans S (M=S-CC) et quel que soit y un sommet de M, on appelle chemin de x à y dans CC tout chemin allant de x à y ne comprenant que des sommets de CC sauf y (voir figure 1.).

Figure 1. Chemins de x à y dans CC.

On note alors distance_x,CC(y), le coût du plus court chemin allant de x à y dans CC et pred_x,CC(y) le prédecesseur de y dans ce plus court chemin.

A chaque étape, on choisit un sommet m de M tel que:

distancex,CC(m) = Min{distancex,CC(y)} 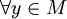$\forall y \in M$

Algorithme

L'algorithme va parcourir le graphe g à partir du sommet source x et retournera deux tableaux: ppd et pr pour mémoriser les plus courts chemins et leur distance respective. ppd[y] mémorisera distance_x,CC(y) et pr[y] mémorisera pred_x,CC(y).

Pour éviter des tests inutiles, nous allons étendre les capacités de la fonction de coût pour qu'elle soit définie quelque soit le couple de sommet (x,y), soit :

coût(x,x,g) = 0 pour un graphe sans boucle


coût(x,y,g) = $\infty$  si x arc y = faux

Nous utiliserons aussi une opération choisirmin(M, ppd) qui renverra le sommet 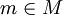$m\in M$ tel que ppd[m] est minimum, ainsi que les opérations sur les ensembles.

Pour l'algorithme de Dijkstra, les types de données employés sont les suivants :

Constantes

   Nbs = ...                           /* Nombre de sommets du graphe */

Types

   t_vectNbsReel = Nbs reel            /* Vecteur de Nbs réels */
   t_vectNbsEnt = Nbs entier           /* Vecteur de Nbs réels */

Ce qui donne:

Algorithme procédure Dijkstra
Paramètres locaux
   entier x                            /* x est le sommet source */
   graphe g
Paramètres globaux
   t_vectNbsRéel ppd                   /* ppd[y] est la distance du plus court chemin de x vers y*/
   t_vectNbsEnt  pr                    /* pr[y] est le prédécesseur de y sur ce chemin */
Variables
   entier i, y, m                      /* y et m sont des sommets */
   réel v
   ensemble M
Début
   /* Initialisation et marquage */
   M $\leftarrow$ ensemblevide
   pour i $\leftarrow$ 1 jusqu'à n faire
      ppd[i] $\leftarrow$ coût(x,i,g)
      pr[i] $\leftarrow$ x
      M $\leftarrow$ ajouter(i,M)
   fin pour
   M $\leftarrow$ supprimer(x,M)                      /* CC={x} */
   /* Ajouts successifs de sommets à CC */
   tant que M <> ensemblevide faire
      m $\leftarrow$ choisirmin(M,ppd)
      si ppd[m] = $\infty$ alors                   /* plus de sommets accessibles depuis x */
         retourne
      fin si 
      M $\leftarrow$ supprimer(m,M)                   /* ajout de m à CC */
      /* réajustement des valeurs de distance */
      pour i $\leftarrow$ 1 jusqu'à do+(m,g) faire
         y $\leftarrow$ ième-succ(i,m,g)
         si y $\in$ M alors                    /* Plus court chemin de x à y pas encore déterminé */
            v $\leftarrow$ ppd[m] + coût(m,y,g)
            si v < ppd[y] alors   
               ppd[y] $\leftarrow$ v
               pr[y] $\leftarrow$ m
            fin si
         fin si
      fin pour
   fin tant que
Fin Algorithme procédure Dijkstra

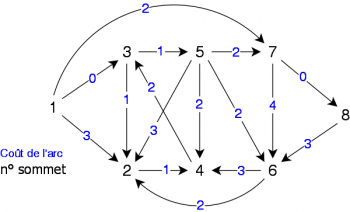
Appliquons l'algorithme de Dijsktra au graphe orienté valué de la figure 2 en prenant le sommet 1 comme sommet source (nous cherchons à déterminer les plus courts chemins depuis 1 vers tous les autres.

Note: les sommets sont traités en ordre croissants, que ce soit dans l'ensemble M ou en tant que successeurs.

Figure 2. Graphe orienté valué G.

Après exécution de l'algorithme dijkstra, nous obtenons les vecteurs ppd et pr suivants (tableau 1) :

Tableau 1. Vecteurs ppd et pr résultants de l'application de l'algorithme de Dijkstra appliqué au graphe de la figure 2.

Sommets (indice)	1	2	3	4	5	6	7	8
PPD	0	1	0	2	1	3	2	2
PR	1	3	1	2	3	5	1	7

Ce qui correspond à l'arbre de racine 1 suivant (voir figure 3):

Figure 3. Arbre des plus courts chemins depuis 1.

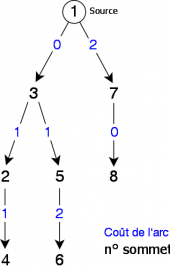
Par exemple, pour connaître le plus court chemin du sommet 1 au sommet 4, il suffit de remonter la parenté depuis le sommet 4 (destination) jusqu'au sommet 1 (la source) en utilisant le vecteur pr. Son coût (plus petite distance) étant obtenu par ppd[4], ce qui donne :

plus court chemin de 1 à 4 : 1$\rightarrow$3$\rightarrow$2$\rightarrow$4 de coût : 2

Bellman

L'algorithme de Bellman est utilisable dans les cas où les coûts des arcs sont quelconques, mais où le graphe ne présente pas de circuit. Il détermine le plus court chemin entre un sommet de départ x (racine du graphe) et tous les autres sommets du graphe accessibles depuis x. On obtient alors un arbre de racine x formé par les plus courts chemins de x vers les sommets qu'il peut atteindre.

Principe

Soit G=< S,A,C > un graphe orienté valué de n sommets. Soit x un sommet de S, on se propose de construire un ensemble CC (court chemin) de sommets y pour lesquels on connait un plus court chemin depuis x. Soit M, complémentaire de CC dans S (M=S-CC), l'ensemble des sommets y pour lesquels ppdistance(x,y,G) n'est pas encore déterminée.

On ne calcule ppdistance(x,y,G) que lorsque tous les prédécesseurs de y sont dans CC.

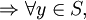$\Rightarrow \forall y \in S,$ il faut connaître son demi-degré intérieur (nombre de prédécesseurs) et pouvoir accèder à son i^ème prédécesseur.

L'idée est la suivante:

Un plus court chemin allant de x à y passe obligatoirement par un des prédécesseurs m de y (voir figure 4), celui pour lequel ppdistance(x,m,G) + coût(m,y,G) est minimum.

Figure 4. Chemins de x à y dans CC.

Algorithme

L'algorithme retournera deux tableaux: ppd et pr pour mémoriser les plus courts chemins et leur distance respective. ppd[y] mémorisera distance_x,CC(y) et pr[y] mémorisera pred_x,CC(y).

Pour éviter des tests inutiles, nous allons étendre les capacités de la fonction de coût pour qu'elle soit définie quelque soit le couple de sommet (x,y), soit :

coût(x,x,g) = 0 pour un graphe sans boucle


coût(x,y,g) = $\infty$  si x arc y = faux

• Au départ, CC ne contient que la source (x).
• A chaque étape L'algorithme choisit donc dans M un sommet y tel que tous ses prédécesseurs soient dans CC. On regarde par lequel de ses prédécesseurs, le chemin depuis x est le plus court. Ce sommet est alors ajouté à CC et les vecteurs ppd et pr sont mis à jour.
• On s'arrête lorsque M est vide.

Nous utiliserons une opération choisirsuivant(M, g) qui renverra un sommet de M n'ayant plus aucun prédécesseurs dans M.

Pour l'algorithme de Bellman, les types de données employés sont les suivants :

Constantes

   Nbs = ...                           /* Nombre de sommets du graphe */

Types

   t_vectNbsReel = Nbs reel            /* Vecteur de Nbs réels */
   t_vectNbsEnt = Nbs entier           /* Vecteur de Nbs réels */

Ce qui donne:

Algorithme procédure Bellman
Paramètres locaux
   entier x                            /* x est le sommet source */
   graphe g
Paramètres globaux
   t_vectNbsRéel ppd                   /* ppd[y] est la distance du plus court chemin de x vers y*/
   t_vectNbsEnt  pr                    /* pr[y] est le prédécesseur de y sur ce chemin */
Variables
   entier i, y, z, m                   /* y, z et m sont des sommets */
   réel min, aux                       /* min et aux sont des distances */
   ensemble M
Début
   /* Initialisation et marquage */
   M $\leftarrow$ ensemblevide
   pour i $\leftarrow$ 1 jusqu'à n faire
      M $\leftarrow$ ajouter(i,M)
   fin pour
   M $\leftarrow$ supprimer(x,M)                      /* CC={x} */
   ppd[x] $\leftarrow$ 0
   pr[x] $\leftarrow$ x
   tant que M <> ensemblevide faire
   /* Ajouts successifs de sommets à CC */
      m $\leftarrow$ choisirsuivant(M,g)
      M $\leftarrow$ supprimer(m,M)                   /* ajout de m à CC */
      y $\leftarrow$ ième-pred(1,m,g)                 /* Premier prédécesseur et sa distance associée */
      min $\leftarrow$ ppd[y] + coût(y,m,g)
      /* comparaison avec les autres prédecesseurs */
      pour i $\leftarrow$ 2 jusqu'à do-(m,g) faire
         z $\leftarrow$ ième-pred(i,m,g)              /* ième prédécesseur et sa distance associée */
         aux $\leftarrow$ ppd[z] + coût(z,m,g)
         si aux < min alors                /* Plus court chemin de x à y pas encore déterminé */
            min $\leftarrow$ aux
            y $\leftarrow$ z
         fin si
      fin pour
      ppd[x] $\leftarrow$ min
      pr[x] $\leftarrow$ y
   fin tant que
Fin Algorithme procédure Bellman

Appliquons l'algorithme de Bellman au graphe orienté valué de la figure 5 en prenant le sommet 1 comme sommet source (nous cherchons à déterminer les plus courts chemins depuis 1 vers tous les autres.

Note: les sommets sont traités en ordre croissants, que ce soit dans l'ensemble M ou en tant que successeurs.

Figure 5. Graphe orienté valué G coûts quelconques (sans circuit).

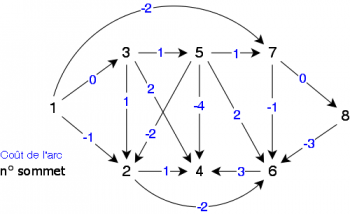
Après exécution de l'algorithme Bellman, nous obtenons les vecteurs ppd et pr suivants (tableau 2) :

Tableau 2. Vecteurs ppd et pr résultants de l'application de l'algorithme de Bellamn appliqué au graphe de la figure 5.

Sommets (indice)	1	2	3	4	5	6	7	8
PPD	0	-1	0	-3	1	-5	-2	-2
PR	1	5	1	5	3	8	1	7

Ce qui correspond à l'arbre de racine 1 suivant (voir figure 6):

Figure 6. Arbre des plus courts chemins depuis 1.

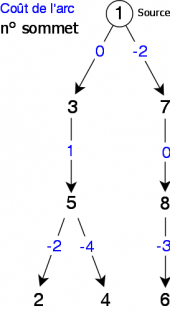
Par exemple, pour connaître le plus court chemin du sommet 1 au sommet 4, il suffit de remonter la parenté depuis le sommet 4 (destination) jusqu'au sommet 1 (la source) en utilisant le vecteur pr. Son coût (plus petite distance) étant obtenu par ppd[4], ce qui donne :

plus court chemin de 1 à 4 : 1$\rightarrow$3$\rightarrow$5$\rightarrow$4 de coût : -3

Floyd

L'algorithme de Floyd est utilisable dans les cas où les coûts des arcs sont quelconques, avec ou sans cirscuits, mais sans circuit absorbant. Il détermine le plus court chemin entre tous les couples de sommet (x,y) d'un graphe G.

Nous pourrions utiliser les algorithmes de Bellman ou de Dijkstra en faisant varier la racine, mais pas pour des graphes à coûts quelconques et présentant des circuits non absorbants.

L'algorithme de Floyd fait partie des algorithmes simples qui déterminent tous les plus courts chemins en utilisant une représentation matricielle.

Principe

Le principe de cet algorithme est le même que celui de l'algorithme de Warshall utilisé pour déterminer la fermeture transitive d'un graphe (connexité du graphe).

Soit G=< S,A,C > un graphe orienté valué de n sommets.

• Au départ, on considère uniquement les chemins de x à y qui ne passent par aucun autre sommet du graphe. On a alors ppdistance(x,y,G) = coût(x,y,G) et pere(x,y,G) = x.
• A chaque étape i, on calcule distance_i(x,y) le coût du plus court chemin allant de x à y passant par des sommets inférieurs ou égaux à i. Si celui-ci est inférieur à la plus petite distance connue actuellement, il devient cette plus petite distance et pere(i,y,G) remplace pere(x,y,G).

Algorithme

L'algorithme utilisera deux matrices: ppd et pr pour mémoriser les plus courts chemins et leur distance respective. ppd[x,y] mémorisera ppdistance_i(x,y) et pr[x,y] mémorisera pere_i(x,y).

Pour éviter des tests inutiles, nous allons étendre les capacités de la fonction de coût pour qu'elle soit définie quelque soit le couple de sommet (x,y), soit :

coût(x,x,g) = 0 pour un graphe sans boucle


coût(x,y,g) = $\infty$  si x arc y = faux

• Au départ, ppd et pr sont initialisés respectivement par coût(x,y,G) et x.
• A chaque étape i, ces deux matrices sont mises à jour par les éventuels plus courts chemins rencontrés passant par des sommets inférieurs ou égaux à i.

Pour l'algorithme qui suit, les type de données employés sont les suivants :

Constantes

   Nbs = ...                            /* Nombre de sommets du graphe */

Types

   t_matNbsNbsréel = Nbs x Nbs réel     /* Matrice réelle carrée de Nbs sommets */
   t_matNbsNbsent = Nbs x Nbs entier    /* Matrice enière carrée de Nbs sommets */

Ce qui donne:

Algorithme procédure Floyd
Paramètres locaux
   graphe g
Paramètres globaux
   t_matNbsNbsréel ppd                  /* Matrice d'adjacence du graphe g */
   t_matNbsNbsent pr                    /* Matrice d'adjacence du graphe g* */
Variables
   entier i, x, y                       /* i, x et y sont des sommets */
Début
   /* Initialisation de ppd et pr */    
   pour x $\leftarrow$ 1 jusqu'à Nbs faire 
      pour y $\leftarrow$ 1 jusqu'à Nbs faire
         ppd[x,y] $\leftarrow$ coût(x,y,g)
         pr[x,y] $\leftarrow$ x
      fin pour
   fin pour

   /* Calcul des plus courts chemins */    
   pour i $\leftarrow$ 1 jusqu'à Nbs faire
      pour x $\leftarrow$ 1 jusqu'à Nbs faire
         pour y $\leftarrow$ 1 jusqu'à Nbs faire
            si ppd[x,i] + ppd[i,y] < ppd[x,y] alors
               ppd[x,y] $\leftarrow$ ppd[x,i] + ppd[i,y]
               pr[x,y] $\leftarrow$ pr[i,y]
            fin si 
         fin pour
      fin pour
   fin pour
Fin Algorithme procédure Floyd

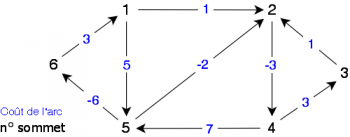
Appliquons l'algorithme de Floyd au graphe orienté valué de la figure 7.

Figure 7. Graphe orienté valué G coûts quelconques et circuits.

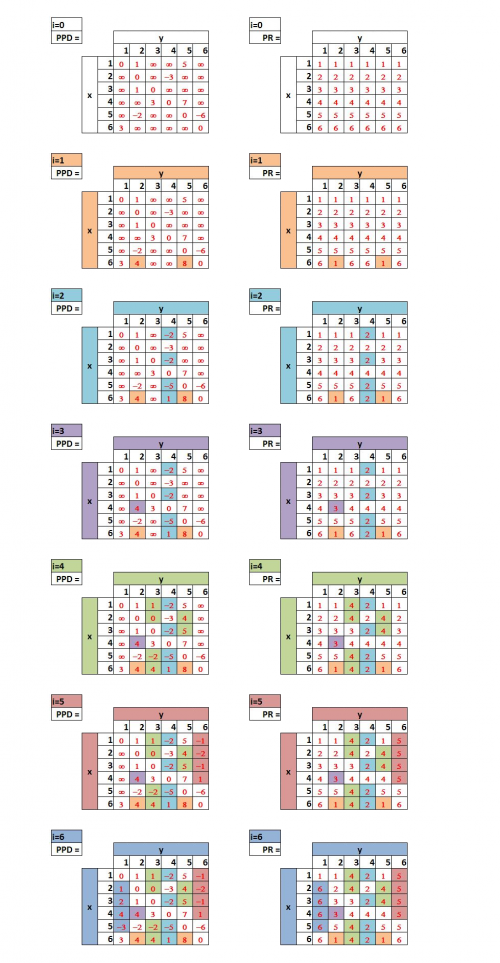
Après exécution de l'algorithme Floyd, nous obtenons les matrices ppd et pr suivantes (tableau 3) :

tableau 3. Evolutions des matrices ppd et pr lors de l'application de l'algorithme de Floyd appliqué au graphe de la figure 7.

Par exemple, pour connaître le plus court chemin allant du sommet 6 au sommet 3, il suffit de remonter la parenté depuis le sommet 3 (destination) jusqu'au sommet 6 (la source) en utilisant le vecteur pr. Son coût (plus petite distance) étant obtenu par ppd[6,3], ce qui donne :

pr[6,3] (4)
pr[6,4] (2)
pr[6,2] (1)
pr[6,1] (6)


Le chemin est donc : 6 -> 1 -> 2 -> 4 -> 3 de coût ppd[6,3] soit 4

---

(Christophe "krisboul" Boullay)