Epita:Algo:Course:Sup-Info:Sets
Contents |
The sets
In addition to checking if an element is in a set, we must be able to:
- insert an element in a set,
- delete an element from a set,
- check if a set is empty,
- etc.
As previously said, we accept the possibility of multiple occurrences of elements (bag). Some representations (to be mentioned later) representations will only be used by sets and others will also be valid for multi-sets. Let us start by giving the abstract algebraic type of the sets.
The set type
types
set
uses
element, boolean
operations
emptyset :set insert : element x set
set delete : element x set
set _
_ : element x set
boolean
For operations insert and Delete, there are two possible behaviors, depending on whether we consider that the element to add is already present or that the element to remove is already absent in the set. This gives the two following possibilities:
- We manage an error, implying that these two operations are partial and in this case require a precondition,
- These two operations are then considered as having no effect.
In the following axioms we will consider the second possibility, that is to say, that the set stays the same after a non effect action.
axioms
xemptyset = false x = y
(x
insert(y, e)) = true x ≠ y
(x
insert(y, e)) = (x
e) x = y
(x
delete(y, e)) = false x ≠ y
(x
delete(y, e)) = (x
e)
We can add the operation that returns the number of elements in a set:
operations
size : setinteger
The latter is defined anywhere, so we have the following axioms:
axioms
size(emptyset) = 0 xe = true
size(insert(x, e)) = size(e) x
e = false
size(insert(x, e)) = size(e) + 1 x
e = true
size(delete(x, e)) = size(e) - 1 x
e = false
size(delete(x, e)) = size(e)
Remark: It would also be possible to add classical set operations such as union, intersection, difference and subset.
Enumeration of a set
In a list to apply the same processing to every element, we use a sequential parsing of the list. In a set, we prefer to choose an arbitrary element, applying the processing to it, deleting it from the set and starting again on the resulting set. So we add a choice operation to the signature of the set type, which gives:
operations
pop : setelement
with the precondition and axiom as follows:
preconditions
pop(e) is-defined-iaoi e ≠ emptyset
axioms
pop(e)e = true
The algorithm processing all the elements of a given set could be the following:
algorithm procedure completeprocessing
Local parameters
set e
Variables
element x
Begin
While e <> emptyset do
x 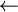 pop(e) /* Choice of x in the set */
process(x) /* Applying of the process to the choosen element */
e
pop(e) /* Choice of x in the set */
process(x) /* Applying of the process to the choosen element */
e 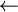 delete(x, e) /* deletion of x */
end while
end algorithm procedure completeprocessing
delete(x, e) /* deletion of x */
end while
end algorithm procedure completeprocessing
Remark: We will see, later in this chapter, the different possible set representations.
Set with repeated elements (bags)
In these cases, the previous operations are preserved, but their behavior differs. Indeed, the addition of an existing element increases the number of elements of the set. Similarly, deleting an item does not mean that it disappears from the set (if there are several occurrences). We then add a new operation (nboccurrences) which allows us to know the number of occurrences of an element in the multiset.
That gives the following algebraic abstract type:
types
multiset
uses
element, boolean, integer
operations
emptymultiset :multiset insert : element x multiset
multiset delete : element x multiset
multiset _
_ : element x multiset
boolean size : multiset
integer nboccurrences : element x multiset
integer
axioms
xemptymultiset = false x = y
(x
insert(y, ms)) = true x ≠ y
(x
insert(y, ms)) = (x
ms) nboccurrences(x, ms) <= 1
(x
delete(x, ms)) = false x ≠ y
(x
delete(y, ms)) = (x
ms)
size(emptymultiset) = 0 size(insert(x, ms)) = size(ms) + 1 xms = true
size(dlete(x, ms)) = size(ms) - 1 x
ms = false
size(delete(x, ms)) = size(ms)
nboccurrences(x, emptymultiset) = 0 x = ynboccurrences(x, insert(y, ms)) = nboccurrences(x, ms) + 1 x ≠ y
nboccurrences(x, insert(y, ms)) = nboccurrences(x, ms) nboccurrences(x, ms) = 0
nboccurrences(x, delete(x, ms)) = 0 nboccurrences(x, ms) >= 1
nboccurrences(x, delete(x, ms)) = nboccurrences(x, ms) - 1 x ≠ y
nboccurrences(x, delete(y, ms)) = nboccurrences(x, ms)
Remarks:
- As for the sets, it would be equally possible to add to the multi-set classical set operations such as union, intersection and difference.
- The enumeration of the elements of a multi-set is done using the same algorithm as for a set. With the deletion removing just one instance of the element, the number of elements corresponds to the total number of elements, all occurrences combined.
Set representations
There are several manners to represent the sets in memory. We will present two of them:
Boolean array implementation
If the possible number of elements N is finite, we can represent a set with an array of N Booleans. That would give the following declaration:
Constants
MaxNb = ...
Types
t_set = MaxNb boolean /* Definition of the boolean array */
Variables
t_set s
If the element i ∈ s then s[i] = true, false otherwise. the "belonging test" to a set is just done looking at the corresponding index, whether it is true or not. The insertion or deletion of an element i is done respectively fixing s[i] to true or false.
Remark:
- These operations are easy and fast to implement because there is only one access to the datum and posibly one value assignment.
- In contrast, the memory cost is important:
- especially if N is large and if few elements of the set are present. The occupancy ratio is very low in this case.
- The empty set is represented by an array in which all elements are false. s result that implies that the initialization of an empty set requires N value assignments.
- Same thing for the complete enumeration of the set.
In this kind of representation, the correspondences between the abstract operations and the static implementation of the type (for a set s) are as follows:
| Abstract type | ⇔ | Boolean array representation |
| insert( x, s) | s[x]=true | |
| delete(x,s) | s[x]=false | |
| x ∈ s | s[x] | |
| emptyset | for i=1 to N do : s[i]=false endfor | |
| size(s) | c=0 for x=1 to N do : if s[x] then : : c=c+1 : endif endfor |
Remark: This representation has to be modified for the multi-sets. Indeed, in this case the Boolean will be replaced by integers giving the number of element occurrences.
List implementation
When the number of possible elements is too large or when the set is infinite, but the sets that are handled are quite small, they can be represented as lists.
In this case a set of N elements is represented by an N elements list.
Remark: Insofar as the order of the elements does not matter, there are several possible lists.
- The "belonging test" of an element x to a set s (the search) is done sequentially through the list comparing x to each element of the set s.
- The insertion of an element x in a set s can be done in two ways:
- insert the element x anywhere in the list (it depends on the chosen representation of the list) without redundancy test,
- insert the element x anywhere in the list (same remark) with an existence test. It will then simplify the deletion and the search of the element.
- The deletion of an element x from a set s can also be done in two ways depending on the choice done for the insertion:
- In the first case, you browse the entire list to make sure you delete all occurrences of the element x.
- In the second case, we can stop as soon as we found the element x.
- The enumeration of a set is also done sequentially browsing the complete list.
In the case of a multi-set:
- The "belonging test" of the element x to a set s is unchanged.
- The insertion of an element x will naturally be done without the existence test of x.
- The deletion of the element x stops at the first occurrence of x encountered.
- For the enumeration too, the whole list has to be browsed. If the number of occurrences of the elements is great, it is necessary to use a couple list < x, nboccurrences(x)>. We then adapt the insertion, deletion and research at this new representation.
Static implementation
The table that we will use must be oversized. To know the current exact number of elements in the set, it is necessary to use a position indicator, for the last element of the set, in the table(their number), which gives:
Constants
MaxNb = 20
Types
t_element = ... /* Definition of element type */ t_vectMaxNbelts = MaxNb t_element /* Definition of element array */ t_set = record /* Definition of type t_set */ t_vectMaxNbelts elts integer nb end record t_set
Variables
t_set s
Using this statement, the different algorithms of set operations are:
Belonging of x to the set s:
algorithm function belong: boolean Local parameters element x set s Variables element i Begin i1 While (i <= s.nb) and (x <> s.elts[i]) do i
i + 1 endwhile return (i <= s.nb) end algorithm function belong
Remark: We can avoid the overflow test (i <= s.nb) positionning a sentinel (the searched element x) at the place s.nb+1. In this way the loop test covers only by the equality of element to x. If we leave the loop at index s.nb+1, this means that x does not belong to the set s.
In this case, the algorithm becomes:
algorithm function belong: boolean Local parameters element x set s Variables element i Begin i1 s.elts[s.nb+1]
x while (x <> s.elts[i]) do i
i + 1 endwhile return (i = s.nb + 1) end algorithm function belong
Insertion of x in the set s with existence test:
algorithm procedure insert_with_test
Local parameters
element x
Global parameters
set s
Begin
if not(belong(x,s)) then
s.nb 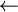 s.nb + 1
s.elts[s.nb]
s.nb + 1
s.elts[s.nb] 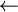 x
endif
end algorithm procedure insert_with_test
x
endif
end algorithm procedure insert_with_test
In this case, the deletion of x from the set s is simple and corresponds to the following algorithm:
algorithm procedure delete_with_test Local parameters element x Global parameters set s Variables element i Begin i1 while (i <= s.nb) and (x <> s.elts[i]) do i
i + 1 endwhile if x = s.elts[i] then s.elts[i]
s.elts[s.nb] s.nb
s.nb - 1 endif end algorithm procedure delete_with_test
Remark: Again, x could be used as a sentinel.
Insertion of x in a set s without existence test:
algorithm procedure insert_without_test Local parameters element x Global parameters set s Begin s.nbs.nb + 1 s.elts[s.nb]
x end algorithm procedure insert_without_test
In this case, the deletion of x from the set s must traverse the whole list to delete all occurrences of x, which corresponds to the following algorithm:
algorithm procedure delete_without_test Local parameters element x Global parameters set s Variables element i Begin i1 while (i <= s.nb) do if x <> s.elts[i] then i
i + 1 else s.elts[i]
s.elts[s.nb] s.nb
s.nb - 1 endif endwhile end algorithm procedure delete_without_test
General remarks:
- The empty set is tested by s.nb = 0. It is sufficient to assign to s.nb the value 0 to represent the abstract operation emptyset.
- In the case of multi-sets:
- We can keep this structure, but we have to use insert_without_test and delete_with_test to manage the multiple occurrences.
- We also can use a couple list < x, nboccurrences(x)> where each element appears several times. In this case, the insertion should either create the non existing couple or increase the occurrence number by 1 if the element already exists. Similarly for the deletion, it suffices to decrease the occurrence number by 1 and to really delete the element if this number reaches 0.
Dynamic implementation
It is sometimes difficult, even impossible, to determine the maximum number of elements of the set. In this case, a static representation (array) is not conceivable and the obvious solution is then the dynamic representation (linked-list). In this case the definition of the type set is as follows:
Types
t_element = ... /* Definition of type element */ t_pset =t_set /* Definition of the pointer on record t_set*/ t_set = record /* Definition of type t_set */ t_element elt t_pset next end record t_set
Variables
t_pset ps
Using this statement, the different algorithms of set operations are:
Belonging of x to the set s:
algorithm function belong : boolean Local parameters element x t_pset s Variables t_pset ps Begin pss while (ps <> NUL) and (x <> ps
.elt) do ps
ps
.next endwhile return (ps <> NUL) end algorithm function belong
Remark: With this representation, using a sentinel requires a direct link to the last element. Without this link it would be necessary to first parse the list of elements completely to place the sentinel. And the cost would obviously be too expensive.
Insertion of x in the set s with existence test:
algorithm procedure insert_with_test
Local parameters
element x
Global parameters
t_pset s
Variables
t_pset ps
Begin
if not(belong(x,s)) then
malloc(ps)
ps .elt
.elt  x
if s = NUL then /* Particular case of an empty set */
ps
x
if s = NUL then /* Particular case of an empty set */
ps .next
.next  NUL /* No next */
else
ps
NUL /* No next */
else
ps .next
.next  s /* Creation of the element on the first place */
endif
s
s /* Creation of the element on the first place */
endif
s  ps
endif
end algorithm procedure insert_with_test
ps
endif
end algorithm procedure insert_with_test
Remark: We could, in case of non existence of the element x, add it at the end of the list because its search leads us to the end of the list.
In this case, the deletion of x from the set s is simple and corresponds to the following algorithm:
algorithm procedure delete_with_test Local parameters element x Global parameters t_pset s Variables t_pset ps, tps Begin pss while (ps <> NUL) and (x <> ps
.elt) do tps
ps /* Memorization of the previous one*/ ps
ps
.next endwhile if x = ps
.elt then if ps <> s then /* Modification of the next link */ tps
.next
ps
.next else /* particular case of the first element */ s
s
.next endif free(ps) /* deletion of the element */ endif end algorithm procedure delete_with_test
Insertion of x in a set s without existence test:
algorithme procedure insert_without_test Local parameters element x Global parameters t_pset s Variables t_pset ps Begin malloc(ps) ps.elt
x if s = NUL then /* Particular case of an empty set */ ps
.next
NUL /* No next */ else ps
.next
s /* Creation of the element of the first place */ endif s
ps end algorithm procedure insert_without_test
Again in this case, the deletion of x in the set s has to parse the list of elements completely to remove all occurrences of x, which gives the following algorithm:
algorithm procedure delete_without_test Local parameters element x Global parameters t_pset s Variables t_pset ps, tps Begin pss while (ps <> NUL) do if x = ps
.elt then if ps <> s then /* Modification of the link of succession */ tps
.next
ps
.next else /* particular case of the first element */ s
s
.next endif free(ps) /* deletion of the element */ endif tps
ps /* Memorization of the previous one */ ps
ps
.next end while end algorithm procedure delete_without_test
Conclusion
In all cases considered there is always at least one operation whose complexity is at worst and on average O(N) where N is either the number of present elements or the number of possible elements. This means that beyond a hundred elements, these methods are no longer possible.